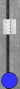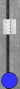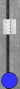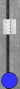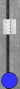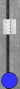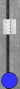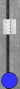The position shown below is uniquely amazing. (It was originally posted by benf with two checkers on Blue's 11pt, but I have modified it.)
There are thirteen Blue checkers on the board. Take the two checkers currently sitting in Blue's bearoff tray and put them on the board on any vacant point that is not in the opponent's outer board. There are six choices: The 12pt, 11pt, 10pt, 9pt, 1pt and 22pt.
A seventh position is created by (a) moving White's 5pt spare to one of the other occupied points in her board and (b) putting the two Blue checkers on one of the above six points. There is only one combination of "a" and "b" (which you need to guess/find) that satisfies the condition set forth in the bold-face sentence below.
Blue has a 32 to play. His 3 is forced (bar/22). With the 2, he can legally move from one of his seven occupied points (except one of the 2s is blocked in the case of owning the 9pt, 1pt or 22pt).
Every legal deuce is the best play for one and only one of each of the seven positions!
.....Position: 12pt, 11pt, 10pt, 9pt, 1pt, 22pt, a+b
.....Deuce: 13/11, 8/6, 6/4, 5/3, 4/2*, 3/1, from floating point.
Your objective is to match the position (on the first line above) with its best deuce (on the second line above).
ANSWERS
Congratulations to Carlo for matching up the deuce to all seven positions correctly! (His only imperfection was minor -- misguessing the placement of White's spare for the seventh position.)
This is not meant to be a complete analysis, but it should lift much of the veil of mystery that otherwise enshrouds this remarkable set of positions.
| 1. | Rollout1 | Bar/22 6/4 | eq: -0.294 |
| Player:
Opponent: | 48.09% (G:13.43% B:0.66%)
51.91% (G:24.42% B:0.27%) | Conf.: ± 0.015 (-0.309...-0.279) - [100.0%]
Duration: 8 minutes 11 seconds |
|
| 2. | Rollout1 | Bar/22 12/10 | eq: -0.352 (-0.058) |
| Player:
Opponent: | 49.97% (G:14.04% B:0.74%)
50.03% (G:32.20% B:0.62%) | Conf.: ± 0.006 (-0.358...-0.346) - [0.0%]
Duration: 4 minutes 51 seconds |
|
| 3. | Rollout1 | Bar/22 8/6 | eq: -0.354 (-0.060) |
| Player:
Opponent: | 48.44% (G:15.58% B:0.81%)
51.56% (G:27.22% B:0.19%) | Conf.: ± 0.011 (-0.365...-0.344) - [0.0%]
Duration: 7 minutes 17 seconds |
|
| 4. | Rollout1 | Bar/22 3/1 | eq: -0.380 (-0.086) |
| Player:
Opponent: | 46.54% (G:12.10% B:0.57%)
53.46% (G:26.71% B:0.43%) | Conf.: ± 0.015 (-0.395...-0.365) - [0.0%]
Duration: 7 minutes 46 seconds |
|
| 5. | Rollout1 | Bar/22 5/3 | eq: -0.430 (-0.136) |
| Player:
Opponent: | 44.27% (G:11.77% B:0.78%)
55.73% (G:27.49% B:0.30%) | Conf.: ± 0.010 (-0.440...-0.420) - [0.0%]
Duration: 7 minutes 33 seconds |
|
| 6. | Rollout1 | Bar/22 4/2* | eq: -0.534 (-0.240) |
| Player:
Opponent: | 42.28% (G:10.75% B:0.44%)
57.72% (G:33.72% B:0.44%) | Conf.: ± 0.008 (-0.542...-0.526) - [0.0%]
Duration: 8 minutes 17 seconds |
|
| 7. | Rollout1 | Bar/22 13/11 | eq: -0.624 (-0.330) |
| Player:
Opponent: | 40.27% (G:9.89% B:0.45%)
59.73% (G:35.11% B:0.63%) | Conf.: ± 0.016 (-0.640...-0.608) - [0.0%]
Duration: 11 minutes 10 seconds |
|
| |
1 1296 Games rolled with Variance Reduction.
Dice Seed: 58946702
Moves: 3-ply, cube decisions: XG Roller
|
Let's start with Blue owning the 12pt, rolled out above. He should (enter and) play 6/4, because of the enormous swing on White's 64. When White is forced to break with 18/8, her equity is –.393. The closest counterpart of that is if she hits and runs with 54 = +.945 or if she rolls 64 when Blue owns the 11pt = +.942; we'll average that counterpart scenario to +.943. The swing on that one roll is therefore .393 + .943 = 1.336 / 18 = .074.
As 12/10 is "only" .049 behind (and 8/6 is only .053 behind), it easy to see that the .074 swing on White's roll of 64 is enough to put the board-breaking 6/4 over the top. The fact that 6/4 leaves 9 fewer shots (11 vs 20) than 8/6 is otherwise insufficient justification to break the board.
| 1. | Rollout1 | Bar/22 5/3 | eq: -0.164 |
| Player:
Opponent: | 51.84% (G:16.08% B:0.86%)
48.16% (G:21.38% B:0.22%) | Conf.: ± 0.010 (-0.174...-0.154) - [100.0%]
Duration: 6 minutes 16 seconds |
|
| 2. | Rollout1 | Bar/22 13/11 | eq: -0.229 (-0.065) |
| Player:
Opponent: | 50.08% (G:15.44% B:0.83%)
49.92% (G:21.32% B:0.13%) | Conf.: ± 0.010 (-0.239...-0.218) - [0.0%]
Duration: 6 minutes 40 seconds |
|
| 3. | Rollout1 | Bar/22 11/9 | eq: -0.322 (-0.158) |
| Player:
Opponent: | 49.74% (G:13.83% B:0.68%)
50.26% (G:26.99% B:0.43%) | Conf.: ± 0.008 (-0.330...-0.314) - [0.0%]
Duration: 5 minutes 58 seconds |
|
| 4. | Rollout1 | Bar/22 3/1 | eq: -0.337 (-0.173) |
| Player:
Opponent: | 47.52% (G:14.15% B:0.66%)
52.48% (G:26.94% B:0.43%) | Conf.: ± 0.009 (-0.345...-0.328) - [0.0%]
Duration: 6 minutes 11 seconds |
|
| 5. | Rollout1 | Bar/22 8/6 | eq: -0.361 (-0.197) |
| Player:
Opponent: | 47.17% (G:15.93% B:0.89%)
52.83% (G:27.32% B:0.21%) | Conf.: ± 0.007 (-0.368...-0.353) - [0.0%]
Duration: 4 minutes 28 seconds |
|
| 6. | Rollout1 | Bar/22 6/4 | eq: -0.414 (-0.250) |
| Player:
Opponent: | 44.81% (G:13.03% B:0.73%)
55.19% (G:28.17% B:0.32%) | Conf.: ± 0.008 (-0.421...-0.406) - [0.0%]
Duration: 5 minutes 57 seconds |
|
| 7. | Rollout1 | Bar/22 4/2* | eq: -0.498 (-0.335) |
| Player:
Opponent: | 43.51% (G:11.82% B:0.54%)
56.49% (G:32.83% B:0.45%) | Conf.: ± 0.008 (-0.507...-0.490) - [0.0%]
Duration: 10 minutes 27 seconds |
|
| |
1 1296 Games rolled with Variance Reduction.
Dice Seed: 18008939
Moves: 3-ply, cube decisions: XG Roller
|
Above is (my rollout of) benf's original (11pt) position.
Following the same theme, Blue should break the 5pt here (5/3). If White rolls 63, she is forced to play 18/9 for an equity of –.329 (according to XGR++ evaluation). If she could hit and run, her equity would basically be +.929. The swing on that one roll is therefore .329 + .929 = 1.258 / 18 = .070.
As 5/3 wins the rollout by "only" .065, we can infer that without the 63 swing roll, the second best play of 13/11 would be best, though barely. (It leaves 5 extra shots but doesn't commit the sin of breaking the board.)
In this position and in the previous position, either of 6/4 or 5/3 (or for that matter 31) gives White a bad 62, and in this position she also has a bad 65. The pivotal issue is to also keep 64 or 63 (whichever it is) bad instead of great. Otherwise, breaking a high point in the board is a dud.
The aspect of being able to more easily recover a point 6-away (while it happens to go hand in hand, and may help one remember) is only of supplemental value. For example, if you move White's 1pt spare back to her 10pt (or 11pt), so that 23/20* 10/4 legally exists, 13/11 becomes the correct deuce and 5/3 a whopper. A little knowledge without understanding is dangerous, because misapplication can result in large errors.
| 1. | Rollout1 | Bar/22 13/11 | eq: +0.065 |
| Player:
Opponent: | 57.73% (G:18.93% B:0.90%)
42.27% (G:14.52% B:0.08%) | Conf.: ± 0.002 (+0.062...+0.067) - [99.9%]
Duration: 45 minutes 04 seconds |
|
| 2. | Rollout1 | Bar/22 5/3 | eq: +0.060 (-0.005) |
| Player:
Opponent: | 58.34% (G:19.39% B:0.97%)
41.66% (G:16.14% B:0.16%) | Conf.: ± 0.002 (+0.057...+0.062) - [0.1%]
Duration: 39 minutes 58 seconds |
|
| 3. | Rollout2 | Bar/22 3/1 | eq: -0.094 (-0.159) |
| Player:
Opponent: | 54.77% (G:17.60% B:0.82%)
45.23% (G:21.00% B:0.31%) | Conf.: ± 0.010 (-0.104...-0.084) - [0.0%]
Duration: 4 minutes 58 seconds |
|
| 4. | Rollout2 | Bar/22 8/6 | eq: -0.107 (-0.172) |
| Player:
Opponent: | 53.84% (G:18.83% B:0.91%)
46.16% (G:19.62% B:0.13%) | Conf.: ± 0.010 (-0.117...-0.097) - [0.0%]
Duration: 5 minutes 15 seconds |
|
| 5. | Rollout2 | Bar/22 11/9 | eq: -0.150 (-0.215) |
| Player:
Opponent: | 53.80% (G:16.17% B:0.84%)
46.20% (G:24.03% B:0.30%) | Conf.: ± 0.011 (-0.161...-0.139) - [0.0%]
Duration: 5 minutes 54 seconds |
|
| 6. | Rollout2 | Bar/22 6/4 | eq: -0.159 (-0.224) |
| Player:
Opponent: | 51.92% (G:15.96% B:0.79%)
48.08% (G:20.59% B:0.22%) | Conf.: ± 0.008 (-0.167...-0.151) - [0.0%]
Duration: 4 minutes 31 seconds |
|
| 7. | Rollout2 | Bar/22 4/2* | eq: -0.300 (-0.365) |
| Player:
Opponent: | 49.10% (G:15.37% B:0.69%)
50.90% (G:27.20% B:0.31%) | Conf.: ± 0.009 (-0.309...-0.291) - [0.0%]
Duration: 12 minutes 36 seconds |
|
| |
1 15552 Games rolled with Variance Reduction.
Dice Seed: 18008939
Moves: 3-ply, cube decisions: XG Roller
2 1296 Games rolled with Variance Reduction.
Dice Seed: 18008939
Moves: 3-ply, cube decisions: XG Roller
|
The difference between this position and the previous position is that White's spare has been moved from her 5pt to her 2pt. (This is the only one of the seven positions where a White checker instead of Blue point is adjusted.)
Why is 13/11 better here (albeit by a mere .005) with White having a 2pt spare, whereas 5/3 is much better (by .065) in the original 11pt position with White having a 5pt spare?
The biggest single reason (accounting for about half the .070 swing) is White's roll of 32, which Blue's 5/3 duplicates when White's spare is on her 6pt or 5pt (or the duped roll is 31 if White's spare is on her 6pt or 4pt). When White's spare is on her 2pt, there is no 32 (or 31) duplication. Another way to look at it is that when Blue plays 13/11, White can resort to hitting inside with 32 (or 31) while keeping a five-point board, whereas when White's spare is on her 2pt, there is no such relief.
The other half of the margin swing can be explained by 53 and 52. (Other swing rolls exist but have less large of an impact and on balance offset what remains.) If the White spare is above her 3pt, she can play the 3 or 2 inside (along with 23/18) without breaking her board. If the spare is below her 3pt, she will leave a double shot on her 16pt or 15pt. Obviously, Blue's subsequent hit rates to be more decisive if his 5pt is covered rather than slotted.
If White's spare is on her 1pt, Blue's 5/3 becomes correct again. This is because when White hits on her 20pt with 31, she no longer has a spare ace to play in her board.
(I have included rollouts when White's spare is on her 5pt or 2pt, but not when it is on her 6pt, 4pt or 1pt.)
| 1. | Rollout1 | Bar/22 10/8 | eq: -0.016 |
| Player:
Opponent: | 57.12% (G:17.52% B:0.97%)
42.88% (G:18.44% B:0.14%) | Conf.: ± 0.009 (-0.025...-0.008) - [100.0%]
Duration: 3 minutes 05 seconds |
|
| 2. | Rollout1 | Bar/22 5/3 | eq: -0.377 (-0.360) |
| Player:
Opponent: | 45.75% (G:13.26% B:0.90%)
54.25% (G:26.63% B:0.30%) | Conf.: ± 0.007 (-0.384...-0.369) - [0.0%]
Duration: 3 minutes 07 seconds |
|
| 3. | Rollout1 | Bar/22 3/1 | eq: -0.405 (-0.389) |
| Player:
Opponent: | 45.38% (G:13.51% B:0.89%)
54.62% (G:28.03% B:0.43%) | Conf.: ± 0.009 (-0.413...-0.396) - [0.0%]
Duration: 3 minutes 33 seconds |
|
| 4. | Rollout1 | Bar/22 6/4 | eq: -0.423 (-0.407) |
| Player:
Opponent: | 44.32% (G:12.34% B:0.61%)
55.68% (G:26.34% B:0.27%) | Conf.: ± 0.009 (-0.432...-0.414) - [0.0%]
Duration: 3 minutes 32 seconds |
|
| 5. | Rollout1 | Bar/22 4/2* | eq: -0.465 (-0.449) |
| Player:
Opponent: | 44.45% (G:12.01% B:0.58%)
55.55% (G:30.30% B:0.41%) | Conf.: ± 0.008 (-0.473...-0.457) - [0.0%]
Duration: 3 minutes 14 seconds |
|
| 6. | Rollout1 | Bar/22 8/6 | eq: -0.479 (-0.463) |
| Player:
Opponent: | 43.24% (G:13.02% B:0.78%)
56.76% (G:28.40% B:0.21%) | Conf.: ± 0.007 (-0.486...-0.473) - [0.0%]
Duration: 2 minutes 04 seconds |
|
| 7. | Rollout1 | Bar/22 13/11 | eq: -0.635 (-0.619) |
| Player:
Opponent: | 39.71% (G:10.41% B:0.52%)
60.29% (G:34.34% B:0.66%) | Conf.: ± 0.018 (-0.653...-0.618) - [0.0%]
Duration: 4 minutes 51 seconds |
|
| |
1 1296 Games rolled with Variance Reduction.
Dice Seed: 34574574
Moves: 3-ply, cube decisions: XG Roller
|
This is the easiest deuce to assign. It is correctly played off the floating point: 10/8. Here, it is possible to expose just one new blot while leaving only 13 shots (compared to 16 shots with 13/11 in the previous position), and there is no break-inside-and-immune-to-6x-hit variation.
[If the roll were 31, Blue should of course break his 4pt, which not only traps 62 off the 18pt but duplicates other 2s as well.]
If Black's floating point is in White's outer board, the correct deuce is of course to split there. Even 14/12 is obvious, as duplication of 5s is a cherry on top. Leaving half a dozen fewer shots by breaking inside is not a serious consideration without a 6-trick.
| 1. | Rollout1 | Bar/22 3/1 | eq: -0.374 |
| Player:
Opponent: | 47.30% (G:13.83% B:0.83%)
52.70% (G:26.48% B:0.39%) | Conf.: ± 0.010 (-0.383...-0.364) - [100.0%]
Duration: 8 minutes 12 seconds |
|
| 2. | Rollout1 | Bar/22 5/3 | eq: -0.440 (-0.066) |
| Player:
Opponent: | 43.79% (G:12.68% B:0.95%)
56.21% (G:27.50% B:0.29%) | Conf.: ± 0.008 (-0.448...-0.431) - [0.0%]
Duration: 8 minutes 47 seconds |
|
| 3. | Rollout1 | Bar/22 6/4 | eq: -0.478 (-0.104) |
| Player:
Opponent: | 42.54% (G:12.18% B:0.74%)
57.46% (G:28.04% B:0.31%) | Conf.: ± 0.009 (-0.487...-0.469) - [0.0%]
Duration: 8 minutes 58 seconds |
|
| 4. | Rollout1 | Bar/22 4/2* | eq: -0.479 (-0.105) |
| Player:
Opponent: | 42.93% (G:11.67% B:0.52%)
57.07% (G:32.05% B:0.47%) | Conf.: ± 0.008 (-0.486...-0.471) - [0.0%]
Duration: 9 minutes 02 seconds |
|
| 5. | Rollout1 | Bar/22 8/6 | eq: -0.506 (-0.133) |
| Player:
Opponent: | 42.25% (G:12.58% B:0.63%)
57.75% (G:28.18% B:0.25%) | Conf.: ± 0.007 (-0.514...-0.499) - [0.0%]
Duration: 5 minutes 53 seconds |
|
| 6. | Rollout1 | Bar/22 13/11 | eq: -0.836 (-0.462) |
| Player:
Opponent: | 36.29% (G:8.65% B:0.46%)
63.71% (G:35.48% B:0.72%) | Conf.: ± 0.015 (-0.851...-0.820) - [0.0%]
Duration: 11 minutes 44 seconds |
|
| |
1 1296 Games rolled with Variance Reduction.
Dice Seed: 34574574
Moves: 3-ply, cube decisions: XG Roller
|
In this case, the lesser of evils is 3/1. If White hits with a 1, she will still be contained by a single-gapped prime (with only 4s to escape).
| 1. | Rollout1 | Bar/22 4/2* | eq: -0.277 |
| Player:
Opponent: | 47.88% (G:14.52% B:0.25%)
52.12% (G:26.29% B:0.46%) | Conf.: ± 0.008 (-0.285...-0.268) - [100.0%]
Duration: 8 minutes 49 seconds |
|
| 2. | Rollout1 | Bar/22 5/3 | eq: -0.327 (-0.051) |
| Player:
Opponent: | 45.41% (G:14.28% B:0.89%)
54.59% (G:21.84% B:0.31%) | Conf.: ± 0.006 (-0.333...-0.321) - [0.0%]
Duration: 6 minutes 59 seconds |
|
| 3. | Rollout1 | Bar/22 6/4 | eq: -0.366 (-0.090) |
| Player:
Opponent: | 44.77% (G:12.57% B:0.51%)
55.23% (G:21.47% B:0.30%) | Conf.: ± 0.006 (-0.372...-0.360) - [0.0%]
Duration: 6 minutes 58 seconds |
|
| 4. | Rollout1 | Bar/22 3/1 | eq: -0.367 (-0.090) |
| Player:
Opponent: | 44.76% (G:13.15% B:0.59%)
55.24% (G:21.92% B:0.34%) | Conf.: ± 0.007 (-0.374...-0.360) - [0.0%]
Duration: 8 minutes 03 seconds |
|
| 5. | Rollout1 | Bar/22 8/6 | eq: -0.446 (-0.169) |
| Player:
Opponent: | 43.22% (G:13.97% B:0.77%)
56.78% (G:20.89% B:0.21%) | Conf.: ± 0.007 (-0.453...-0.439) - [0.0%]
Duration: 4 minutes 55 seconds |
|
| 6. | Rollout1 | Bar/22 13/11 | eq: -0.748 (-0.471) |
| Player:
Opponent: | 36.24% (G:10.46% B:0.48%)
63.76% (G:30.37% B:0.84%) | Conf.: ± 0.013 (-0.760...-0.735) - [0.0%]
Duration: 8 minutes 20 seconds |
|
| |
1 1296 Games rolled with Variance Reduction.
Dice Seed: 58946702
Moves: 3-ply, cube decisions: XG Roller
|
Blue's extra point in the board is enough to make 4/2* (hitting) easily the best play. Now White fans instead of hitting with 31 11 or coming out (bar/18) with 61. Moreover, it is much easier for Blue to make his fifth and sixth inside points with the 1pt already made.
| 1. | Rollout1 | Bar/22 8/6 | eq: -0.349 |
| Player:
Opponent: | 47.75% (G:13.48% B:0.64%)
52.25% (G:26.41% B:0.42%) | Conf.: ± 0.004 (-0.353...-0.345) - [100.0%]
Duration: 31 minutes 53 seconds |
|
| 2. | Rollout1 | Bar/22 5/3 | eq: -0.382 (-0.033) |
| Player:
Opponent: | 45.20% (G:12.43% B:0.59%)
54.80% (G:26.50% B:0.62%) | Conf.: ± 0.005 (-0.387...-0.377) - [0.0%]
Duration: 55 minutes 34 seconds |
|
| 3. | Rollout1 | Bar/22 6/4 | eq: -0.389 (-0.040) |
| Player:
Opponent: | 44.83% (G:12.56% B:0.61%)
55.17% (G:26.10% B:0.52%) | Conf.: ± 0.005 (-0.394...-0.384) - [0.0%]
Duration: 53 minutes 17 seconds |
|
| 4. | Rollout1 | Bar/22 3/1 | eq: -0.393 (-0.044) |
| Player:
Opponent: | 45.41% (G:12.17% B:0.53%)
54.59% (G:28.00% B:0.76%) | Conf.: ± 0.005 (-0.399...-0.388) - [0.0%]
Duration: 20 minutes 21 seconds |
|
| 5. | Rollout2 | Bar/22 13/11 | eq: -0.582 (-0.233) |
| Player:
Opponent: | 41.50% (G:10.43% B:0.45%)
58.50% (G:36.62% B:0.78%) | Conf.: ± 0.008 (-0.590...-0.574) - [0.0%]
Duration: 3 minutes 46 seconds |
|
| 6. | Rollout2 | Bar/22 4/2* | eq: -0.599 (-0.250) |
| Player:
Opponent: | 40.23% (G:10.23% B:0.40%)
59.77% (G:36.49% B:0.82%) | Conf.: ± 0.019 (-0.618...-0.580) - [0.0%]
Duration: 5 minutes 59 seconds |
|
| |
1 5184 Games rolled with Variance Reduction.
Dice Seed: 98939349
Moves: 3-ply, cube decisions: XG Roller
2 1296 Games rolled with Variance Reduction.
Dice Seed: 98939349
Moves: 3-ply, cube decisions: XG Roller
|
The problem with breaking inside here (6/4, 5/3 or 3/1) is that Blue is relatively worse off both when he gets hit and when he doesn't get hit. Against that, White leaves 9 fewer shots (11 vs 20) out of 36, making this a sensitive tradeoff.
Let's compare the top two candidates: 8/6 to 5/3, starting with the HITS: If White hits after 8/6, her average equity is .777. If White hits after 5/3 her equity is .997, the rise being attributable to Blue's open 5pt. As 20 x .777 is greater than 11 x .997, the quantity of hits is of greater concern than the quality of hits, by 4.57. Dividing that by 36 yields a margin of .127, and hence if one confines oneself only to immediate-hit variations, one would conclude that 5/3 is best and 8/6 is a whopper.
I'll use three paragraphs to analyze the NON-HITS. After 8/6, White's 16 non-hits break down as follows: 3 numbers (42 33) break the board and stay back on the 23pt; 3 additional numbers (44 22 43) stay back; 8 numbers (32 52 53 54) leave a direct shot; and 1 number (55) is safe. According to XGR++ evaluation, White's average equity (despite owning the cube) over these 16 missing numbers is –.112, due to Blue's superior timing and outfield control. That comes to –.112 x 16 = –1.79. Combining that with the 4.57 above nets a remainder of 2.78, so far.
The most interesting variations are when Blue plays 5/3 and White misses (25 numbers). White is induced into breaking her 18pt with 10 numbers (65 64 62 42 41), but Blue is unable to reap much benefit (equity of only .079 on average) because his 5pt is downgraded from covered to slotted. Indeed, White much prefers to (yee-hah) break her 18pt with 42 (and 41) instead of breaking her board as she is compelled to do against 8/6. Factoring in also the sole board-breaking number of double aces (+.112) raises the total make-up back to 2.78 + (.079*10) + .112 = 3.68.
What remains is White's 14 positive non-hits vs 5/3 -- "normal" numbers that neither hit nor do anything conceptually terrible. Accounting for Blue's inferior board, these non-hits range from the roll of 21 (.100) up to 55 (.780), with 66 61 44 22 51 54 52 ranked in between, which average +.346 and thus sum to 4.84. That figure surpasses 3.68 (the "make-up" accumulated from the previous paragraph).
When you subtract 3.68 from 4.84 and divide by 36 you end up with a margin of .032 in favor of 8/6. This agrees closely with the 5k rollout margin of .033 (+/– .005) displayed above.
In summary, here is a list of the seven positions, each matched to the best deuce.
.....Blue owns his 12pt......6/4
.....Blue owns his 11pt......5/3
.....B 11pt, W spare 2pt...13/11
.....Blue owns his 10pt.....10/8
.....Blue owns his 9pt........3/1
.....Blue owns his 1pt........4/2*
.....Blue owns his 22pt......8/6
Welcome back, Lady Laila :)
Nack