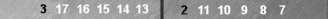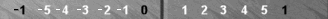This is post #2 of the Naccel 2 series. It is in reponse to Ian's post, though I am writing for the general readership as well.
Thanks, Ian for your comments and position.
Traditional pip-counting is analogous to walking. Cluster counting is analogous to running. The beauty of Cluster is that it builds on movements you already know and enhances them.
Naccel is analogous to skating. Itís faster than walking or running, but not at the beginning. You have to learn how to (a) use the skates properly first and (b) practice. (Neither is much good without the other.) That can be tough if nobody is around to show you how to balance, etc., and in addition you have never seen anyone skate: you donít even know that skating really is faster. It is only natural to lose confidence and go back to running.
Later in this post, youíll understand enough so that you can watch me skate, and that might interest you enough to try skating yourself (as you have never really skated to begin with).
Below is the position you sent.
| |
|---|---|
First, review the Supers (Super-points), shown in post #1 (first diagram). Now note that in your position here (above), Blueís back checkers sit on S3 (Super 3) and S2 (Super 2). Thatís a count of 3 + 2 = 5 on the far side.
Next, here's a valuable tip: the way to count a stack of six checkers on a point is simply by the point number. For example,
| Six-stack = Point number! | |
|---|---|
| |
| 3 | |
The trad 6pt is the 0pt in Naccel (marked "0" above). To its right is the 1pt, then the 2pt, and then the 3pt, marked "3."
Six checkers on the (Naccel) 3pt count "3." That's all there is to it.
Okay, now consider the formation below:
| Six-symmetry = Point number! | |
|---|---|
| |
| 3 | |
Okay, now go back and look at your original full-board position. It is made up almost entirely of two components. (a) The 3 + 2 = 5 count on the far side, and (b) the 3 count on the near side (just shown). As the 0pt (trad 6pt) checkers are invisible (they count zero), all that remains are two checkers on the 1pt, which are 2 pips.
In short, Blue's count is 5 + 3 = 8, with 2 pips left over. I typically write this as 8(2). (Other choices are 8:2 and 8s2p.)
For reference, the two main subparts of your Blue count are shown below, with the 2 extra pips in the third diagram. (Subcounts are shown in the lower right.) Then we'll move on to White's count.
| |
|---|---|
| 5 | |
| |
|---|---|
| 3 | |
| |
|---|---|
| (2) | |
Okay, now let's count White. The position, again, is:
| |
|---|---|
| 9(1) | |
|---|---|
| |
| Three on S3, plus a pip = 9(1) | |
All that remain are White's three back checkers. The one on the roof is just 1 pip away from S3; she therefore has three on S3 = 9, plus a pip. Her count is 9(1).
With Blue's pipcount being 9(1) and White's being 8(2), Blue trails by 5 pips (one shy of a super-pip or supe). That should tell you all you need to know.
If you want trad totals for some reason, 9*6 + 1 + 90 = 145, and 8*6 +2 +90 = 140.
This series of posts will continue as long as reader enthusiasm continues (and assuming I can continue to make the time). Someone can send another position to count, if/when s/he likes.
Cheers,
Nack