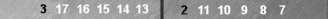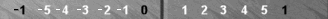Welcome to Naccel 2 -- post #5.
If you would like to catch up or review earlier material:
Post #1, Post #2, Post #3,
Post #3x, Post #4, Post #4x.
As always, Naccel point numbers are labeled in white, Super (Super-point) numbers in black.
Iíll start by showing you how to count a six-point prime:
| |
|---|---|
| Six-prime | -3 |
[You can also choose to count this formation as two six-syms: one around the -3pt and the other around the 0pt. This essentially adds together the second and fifth points of the prime. Yet another option is to sum the middle points: -2 and -1 sum to -3.]
Letís apply that nugget of knowledge to the first of the two positions submitted by Jim:
| |
|---|---|
| |
|---|---|
| 4(1) | |
[If you know (as I did) that an S3 blot (+3) offsets/poofs this six-prime (-3), the count is even shorter: 4 for S2, plus 1 pip to enter the roofer.]
On to Whiteís position. It can be divided into two groups. The first is
| Poof | 0 |
|---|---|
| |
This means White has only five checkers (shown below) that you actually need to count.
| |
|---|---|
That "five-sym" mixed fraction count is either advanced or hard to find, so instead I'll suggest to you this 2-pip shift:
| Zag plus 5 pips | 5(5) |
|---|---|
| |
A zag counts 5, plus 5 pips for the blot; White's entire count is 5(5).
Recapping both sides: Blue is ahead 4(1) to 5(5), which is a lead of 1(4), or 10 pips.
Okay, now for Jimís second position:
| |
|---|---|
| |
|---|---|
| Closed board plus 2 pips | -5(+2) |
Now, Whiteís position:
| -11(+2) | |
|---|---|
| |
Ian chose to view Whiteís two checkers as symmetrical around the midpoint -- equivalent to having them on the midpoint = 2(2). Then he subtracted the 13 borne off, achieving the same -11(+2) result.
(Ian's choice relates to the method described for bundling five White checkers, four diagrams back. The shift is easy to see here if you "hop" the roofer +2 and back-hop the other checker -2, so that they meet on the midpoint. Hopping is a valuable visual aid that will be explained later in this post.)
[When the set of checkers as a whole is closer to S-1 (the bearoff tray) than to S0, a reasonable option is to bump up the Supers by 1 so that S0 is the bearoff tray). However, I strongly advise against adding this wrinkle until your regular S0 counts feel confident and natural.]
This time, we have a third position, submitted by Ian.
| |
|---|---|
| |
|---|---|
| Mirror plus twelve-sym, minus 2 pips | -6(-2) |
If you donít see how two six-syms are symmetrical around the -4pt, picture two three-primes on top of each other (for example). If you donít understand why a three-prime is a six-sym or donít know how to identify or count a six-sym, review the second and third diagrams here, the second diagram here, and the fifth diagram here. If you don't know how to identify or count a mirror, review the third and fourth diagrams here and the eighth diagram here.
[Alternatively, you can poof the 2pt and -2pt blots, count the twelve-sym as -8, and add back in 1(4) for the far-side checker, resulting in -7(+4). That agrees with the -6(-2) count above.]
Before we count Whiteís position, Iíll introduce you to a technique called ďhopping.Ē
| Visualize three hops | 3 |
|---|---|
| |
The third way is to "hop." A hop is a visualized movement of one supe (6 pips), counting +1 for each forward hop or -1 for each backward hop. Having seen and played a lot of double 6s over the years, we all hop naturally.
By hopping around the board in the above diagram, White's roofer will land on her own bar point (Naccel 1pt). How convenient! This creates a little poof, the checker on the 1pt and -1pt cancelling each other out. (I trust you can visualize the position after White's triple-hop without the aid of an after-diagram.)
Returning to the main position:
| |
|---|---|
| Closed board (and a tiny poof) | -5 |
|---|---|
| |
Hopping will open whole new worlds of understanding and speed counting to you. In this case, if you know/remember that roofer + -1pt checker = 3, great. If you don't know or forget, then hop, and you'll be more likely to remember the instant 3 count of that little formation for next time.
Recapping, Blueís count is -6(-2) and Whiteís count is -2(+3). Blue leads by 4(5).
Next position?
Nack