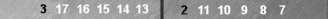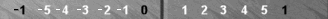Welcome to post #7 of the Naccel 2 teaching series.
For review, click on the following:
FAQ, Post#1, Post#2, Post#3, Post#3x,
Post#4, Post#4x, Post#5, Post#5x, Post#6, Post#6x.
The current post (#7) is in response to Matt Ryder's post entitled Learning Naccel - Problem 1.
I applaud your courage, Matt, and the fine example you set :)
Here is your position:
| 7 | |
|---|---|
| |
| 2 | |
That said, I want to suggest an even faster idea: "Hop" the blot down to n2, as shown below. (To review hopping, see the twelfth diagram here.
| |
|---|---|
| Big poof + Pair, or Small poof + Six-prime | 1 |
The other way is to poof only the spares, and count the six-prime: sum the endpoints (i.e., -2 + 3 = 1), or, alternatively, double the high point and subtract 5 (i.e., 3*2 - 5 = 1). Either way, you add that 1 to the +1 hop, achieving the total of 2.
For you, hopping is best (assuming you notice the thirteen-checker poof), and then it mostly comes down to which of the pair or six-prime you can count faster, or spot first. (In time, this pair and six-prime will each be an obvious, instant count of 1 to you, so it won't matter.)
A supplemental lesson here is that when you see a poof, quickly check to see if there might be an even bigger one.
Now I'll share with you the way I counted Blue (first with a prep diagram).
| |
|---|---|
| Blot Diag | 1 |
Let's repeat the full position for Blue:
| |
|---|---|
| Six-prime and Blot Diag | 2 |
To be clear, I don't expect you to spot the diag (instead of shifting or hopping) or to count the six-prime as an instant 1 until you've had more practice: I'm just giving you a glimpse of two of the many corners you will eventually cut.
Let's repeat the position below and count for White.
| 7 | |
|---|---|
| |
| 2 | |
| Block and Closed board | 6 |
|---|---|
| |
That's clever, Matt! The block counts (16 + 17) / 3 = 11, and the closed board (counted like any other six-prime) is -5, for a net count of 6.
The only problem, as Petter said, is that you forgot to add 1 for the checker you conjured from S-1. (If you like, think of it this way: either (a) you "hopped" a checker from S0 to S-1, adding 1 to the count, then performed your 1-pip shift; or (b) your countershift was from n0 to n1 and then you hopped forward, closing the board.) Had you done so, you would have gotten the correct count of 7.
If you don't want to deal with the hop, you can do this shift instead:
| Block, Triplet and Sym | 7 |
|---|---|
| |
For clarity, I made the (irrelevant) S0 checkers invisible. The block is still 11, the triplet is -2 (half of its point number, as illustrated in the seventh diagram here) and the six-sym around n-2 is -2, for a count of 11 - 2 - 2 = 7.
Btw, I call White's nine-checker squad a "truck" (which counts the point number of its cab plus thrice the Super adjacent to its rear). I know this truck as -4, so I don't need to separately add the triplet and six-sym. My count would be a bit shorter: 11 - 4 = 7.
Petter's count is cool, too. From the main position (three diagrams back), he counted the six-sym around n-2 as -2, and n16 plus n-4 as a point mirror of 4. However, he did more work than necessary when he shifted n17 and n-5 to the Supers; these blots are already mirrored. Instead, (after counting the six-sym of -2), it is better to count the S3 blot as it is, leaving the six-checker mirror formation shown below:
| Six-checker mirror | 6 |
|---|---|
| |
Jim -- as you suspect, spotting mirror-family formations for White is just a matter of practice. I don't stutter in the slightest when going back and forth from Blue counts to White counts.
Matt -- negative numbers are your friend. That is what allows you to poof so many checkers and that is why all the numbers in Naccel are so small. Don't be overly concerned with left-over counts; once you're counting right you'll get down to having one left at the end (positive or negative). Then again, I think you already know that, intuitively :)
Finally, I'll show you how I chose to count White.
I find the following to be a handy poof:
| Poof (S3 and -3 sym) | 0 |
|---|---|
| |
After poofing the above (to me, standard) seven-checker formation (and of course S0 is poofed too), and therefore having had to count nothing so far, I was left with these six checkers:
| Blot mirror, and zag | 7 |
|---|---|
| |
To review mirrors, see the third and fourth diagrams here. To review zags, see the eighth and ninth diagrams here or the sixth diagram here (zag for White).
Nack