I think those who responded either did not catch that that I changed player names to Human1 and Human2, or did not think it mattered. I made a bold play here, knowing it was wrong. But I think bold play could be practically correct against average human. The main reason is how they handle redoubles at this score. What is not a money double could be a huge pass. I post the rollout of original problem first, followed by position where I redoubled, my opponent took, and I won a gammon for the match.

  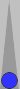 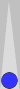           
 | | White is Player 2
score: 9
pip: 104 | | 13 point match | pip: 135
score: 6
Blue is Player 1 |
| | XGID=--AAB-D-BB-a---c-c-dBb-bA-:1:1:1:54:6:9:0:13:10 | | Blue to play 54 | | | 1. | Rollout1 | 8/3 6/2 | eq: -0.2535 | | Player:
Opponent: | 30.81% (G:5.27% B:0.09%)
69.19% (G:7.55% B:0.27%) | Conf.: ±0.0062 (-0.2597...-0.2472) - [100.0%]
Duration: 2 minutes 50 seconds |
| | 2. | Rollout1 | 20/11* | eq: -0.2761 (-0.0226) | | Player:
Opponent: | 35.29% (G:7.58% B:0.48%)
64.71% (G:32.04% B:6.98%) | Conf.: ±0.0119 (-0.2880...-0.2642) - [0.0%]
Duration: 3 minutes 40 seconds |
| | | 1 1296 Games rolled with Variance Reduction.
Moves and cube decisions: 3-ply
|
|
eXtreme Gammon Version: 2.01, MET: Rockwell-Kazaross

              
 
       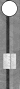       
 | | White is Player 2
score: 9
pip: 109 | | 13 point match | pip: 129
score: 6
Blue is Player 1 |
| | XGID=aB-BC-CA-------ba-ccCc-bA-:1:1:1:00:6:9:0:13:10 | | Blue on roll, cube action? | | | Analyzed in XG Roller+ | No redouble | Redouble/Take | | Player Winning Chances: | 59.127% (G:27.980% B:0.394%) | 59.010% (G:28.673% B:0.363%) | | Opponent Winning Chances: | 40.873% (G:10.670% B:0.643%) | 40.990% (G:11.434% B:0.829%) | | Cubeless Equities | +0.3772 | +1.2833 | | Cubeful Equities | | No redouble: | +0.7389 (-0.2611) | | | Redouble/Take: | +1.2833 (+0.2833) | | | Redouble/Pass: | +1.0000 | | | | Best Cube action: Redouble / Pass |
|
eXtreme Gammon Version: 2.01, MET: Rockwell-Kazaross