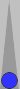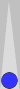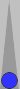                        |
| ||||
| XGID=-ECC--A----AA---A--eccac--:0:0:-1:00:0:0:3:0:10 | |||||
| White on roll, cube action? | |||||
| Analyzed in Rollout | No double | Double/Take |
| Player Winning Chances: | 84.61% (G:0.04% B:0.00%) | 84.62% (G:0.04% B:0.00%) |
| Opponent Winning Chances: | 15.39% (G:0.00% B:0.00%) | 15.38% (G:0.00% B:0.00%) |
| Cubeless Equities | +0.693 | +1.385 |
| Cubeful Equities | ||
| No double: | +0.928 (-0.072) | ±0.001 (+0.927..+0.929) |
| Double/Take: | +1.296 (+0.296) | ±0.002 (+1.293..+1.298) |
| Double/Pass: | +1.000 | |
| Best Cube action: Double / Pass | ||
| Rollout details | ||
| 2592 Games rolled with Variance Reduction. Dice Seed: 92034934 Moves: 3-ply, cube decisions: XG Roller | ||
| Double Decision confidence: | 100.0% | |
| Take Decision confidence: | 100.0% | |
| Duration: 20.2 seconds | ||
eXtreme Gammon Version: 2.10
Thanks to all who posted on this. These races have been a problem for me, and I now feel much better equipped for them.
Here is a summary of what I've learned from you:
Here is a summary of what I've learned from you:
1. Walter Trice gave an EPC formula for stack and straggler positions on page 141 of Boot Camp: EPC = (3.5 * #ofCheckers) + Straggler pip count.
He also offered a "rough-and-ready" EPC cube action rule for pips v rolls on page 140: Point of last take for trailer is when down a number of Effective Pips equal to number of rolls to go minus three.
2. Some posters referenced a -4 pip correction for two stragglers. I cannot find where Walter wrote this. (Can anyone provide a reference?)
3. Smcrtorchs provided a table for how to extend the stack and straggler formula to more stragglers:
Judging the original position as a stack (extended to the 2 and 3 points) with 4-stragglers yields a quite-accurate EPC of 86.
- 1 straggler : 3.5*(number of checkers) + straggler pipcount.
- 2 stragglers: subtract 4 from pip count.
- 3 stragglers: subtract 6.5.
- 4 stragglers: subtract 10.
Judging the original position as a stack (extended to the 2 and 3 points) with 4-stragglers yields a quite-accurate EPC of 86.
4. John O'Hagan described a neat trick: pretend your two calculated EPCs are from positions with nice distributions. Since nice distributions typically have 7.5 pips wastage, subtract 7.5 from each EPC to derive an associated raw pip count. This has value since we know lots of nice formulas for raw pip counts, and can perhaps avoid using new formulas for judging EPC-based cube action. Let's redo this, but using the better EPC value we got just above:
- White's raw pip count is 66. Add one for extra checker on deuce: 67.
- Blue's EPC is 86. Subtract 7.5 for an associated raw pip count of 78.5.
- Normal point-of-last-take for 67 pips is 8 pips down = 75 pips. Blue is 3.5 pips worse, so clear money pass. Estimate 2% fewer wins for each pip past point of last take = 7% below 23% for 16% raw winning chances.
- Actual winning chances: 15.4%
5. Paul Weaver demonstrated a fun method for estimating the EPC of an oddball position OTC (over the computer):
Find a "normal" position of known EPC that has equal winning chances against the oddball position depending on who rolls first. This is a nice extension of Walter's position on page 140 of Boot Camp:
Find a "normal" position of known EPC that has equal winning chances against the oddball position depending on who rolls first. This is a nice extension of Walter's position on page 140 of Boot Camp:
   |
| ||||
| XGID=-EEE---------------cdc----:0:0:1:00:0:0:3:0:10 | |||||
| Blue on roll, cube action? | |||||
eXtreme Gammon Version: 2.10
Walter showed that both positions have EPCs of about 57. Paul extended this idea from pips v rolls to pips v stack-and-stragglers. Nice. 6. Mr Majestyk used a non-EPC method: He used Keith-count adjustments for checkers on the ace and deuce, and gaps on the 4 and 5, plus another 7 pips to get a first estimate of winning chances. Then he added 21% of the outfield checkers distance to the 6-point and 0.5% for each outfield crossover to the favorite's winning chances.