BGonline.org Forums

Rollout + several bonuses

Posted By: Timothy Chow
Date: Tuesday, 22 April 2014, at 1:13 p.m.

In Response To: Break anchor to hit? #3 (Timothy Chow)

You may or may not have found this specific problem easy, but certainly this class of problems—breaking anchor to hit when your opponent has no checkers back and you have one or more blots in your board—is a very difficult one to master, and I'm surprised that I haven't seen more examples of it discussed in books and articles. The difference in wins and gammons between the candidate plays can be enormous, making the tradeoff difficult to evaluate even for money, let alone at some funny match score. Many variations can arise that are not easily captured in a simple rule or a small set of reference positions. The best I can do at the moment is to collect several examples and offer a few observations.

In the position at hand, since Blue is somewhat ahead in the race, the safe play of advancing the anchor is definitely worth considering. The pseudocubeless numbers suggest, however, that hitting not only wins somewhat more games, but wins a lot more gammons.

		White is Player 2 score: 0 pip: 133 Unlimited Game pip: 134 score: 0 Blue is Player 1
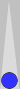XGID=-B-AB-C-BabacB---b-bBA-bb-:0:0:1:65:0:0:0:0:10
Blue to play 65

1.	Rollout1	20/9*	eq: +0.385
	Player: Opponent: 58.09% (G:29.79% B:0.79%) 41.91% (G:14.01% B:0.76%) Conf.: ± 0.013 (+0.372...+0.398) - [100.0%] Duration: 12 minutes 45 seconds
2.	Rollout1	21/15 20/15	eq: +0.262 (-0.123)
	Player: Opponent: 56.96% (G:15.56% B:0.36%) 43.04% (G:8.96% B:0.26%) Conf.: ± 0.015 (+0.247...+0.276) - [0.0%] Duration: 15 minutes 33 seconds
1 1296 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller

eXtreme Gammon Version: 2.10

---

Here's another example with a similar flavor that arose in a different game of mine. The race is even and both sides have a three-point board, with Blue having a blot in his board. This time, though, Blue's alternative isn't as appealing, and the pseudocubeless numbers indicate that the advantage of hitting comes from the extra games won, not the gammons.

		White is Player 2 score: 0 pip: 113 Unlimited Game pip: 117 score: 0 Blue is Player 1
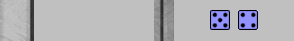XGID=-B-CA-B-C-b-bB--ab-cBc--b-:0:0:1:54:0:0:0:0:10
Blue to play 54

1.	Rollout1	20/16* 16/11	eq: -0.089
	Player: Opponent: 47.50% (G:18.15% B:0.55%) 52.50% (G:21.30% B:0.80%) Conf.: ± 0.012 (-0.101...-0.076) - [100.0%] Duration: 10 minutes 35 seconds
2.	Rollout1	13/9 13/8	eq: -0.236 (-0.147)
	Player: Opponent: 43.83% (G:3.94% B:0.09%) 56.17% (G:4.23% B:0.28%) Conf.: ± 0.009 (-0.245...-0.228) - [0.0%] Duration: 9 minutes 29 seconds
1 1296 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller

eXtreme Gammon Version: 2.10

---

As I mentioned over on rec.games.backgammon when this topic came up recently, a more dramatic example of this type of decision was posted here on BGO Mislav Kovacic a few years ago. I'm reproducing the position below for convenience; click here for the rollout.

Match to 7, Tied at 0-0
Blue to play 65

White	112
Blue	110
GNUBg Id: Zm5DCwCtthkADA:cIn6AAAAAAAA XGID=-ABAABBB-B-aba---bbc-bBb--:0:0:1:65:0:0:0:7:8

---

Here's another one from one of my old "Checkerplay Challenges" where Blue is far behind in the race; click here for the rollout (see Problem 3).

Money Game
Blue to play 22

White	63
Blue	99
GNUBg Id: t5sTBABtu0QAAw:UQkJAAAAAAAA XGID=-ABBBCA-A--Aa----a-cBbcbc-:1:1:1:22:0:0:0:0:10

---

Lest you think that it's always right to hit in such situations, in the aforementioned discussion on rec.games.backgammon, smcrtorchs posted an interesting example from Mochy–Phipps (San Antonio 2014) where the computer dings Mochy's choice to hit. (Though strictly speaking this position doesn't quite fit the description I gave above because White has an anchor; that does make a difference.)

Match to 11, Blue leads 5-0
Blue on roll. Cube action?

Phipps	125
Mochy	149
GNUBg Id: zG4HAQNqzuAABw:cAlgAQAAKAAA XGID=--AABbC-B---aC---cbcbCb---:0:0:1:00:5:0:0:11:16

Messages In This Thread

• Break anchor to hit? #3
  Timothy Chow -- Sunday, 20 April 2014, at 6:16 p.m.
  • Break anchor to hit? #3
    Taper_Mike -- Sunday, 20 April 2014, at 8:26 p.m.
  • Break anchor to hit? #3
    Fatboy -- Sunday, 20 April 2014, at 11:14 p.m.
  • Break anchor to hit? #3
    ah_clem -- Monday, 21 April 2014, at 12:07 p.m.
  • Rollout + several bonuses
    Timothy Chow -- Tuesday, 22 April 2014, at 1:13 p.m.