[ View Thread ] [ Post Response ] [ Return to Index ] [ Read Prev Msg ] [ Read Next Msg ]

BGonline.org Forums

Four Score and Seven Years ago...

Posted By: Nack Ballard
Date: Sunday, 21 December 2014, at 1:26 a.m.

A "four-score position" is one (based on the highest quality rollouts that today can be performed practically) for which a different play is best at each of the four classically recognized main scores: m, d, s, and g [which respectively stand for Money (center cube strongly preferred), DMP, gammon save, and gammon go]. These positions are subdivided into two types: "T4" (technical four-score) and "R4" (real four-score).

For a "T4," it is necessary only for each best play to "win" its high quality rollout (i.e., with strong settings, and with enough trials to achieve 100% confidence), no matter by how tiny a margin. Only one T4 has been found as early as the second roll, which is 63S-32, where the best plays at m, d, s and g win the long 4-ply rollouts (over their respective second best moves) by .0018, .0003, .0054 and .0013.

The requirements for an "R4" are more stringent. At each score, the best play cannot be "tied" with the second best play, as defined by the B/W (Ballard/Weaver) error scale published on the final page of Backgammon Openings. The B/W scale states that any play within .01 is tied for Money. According to my empirical research, that translates to .0045 at DMP, and to .007 at gammon save and gammon go. If all four of these equity-difference cusps (.01, .0045, .007, .007) are surpassed, the position qualifies as an R4.

Seven years ago, the pioneer R4 (real four-score position) was published on pages 98–99 of Backgammon Openings (see link above). It had been verified by lengthy GnuBG rollouts. When XG came along, it overturned one of Gnu's rollouts (done with version 14.3 devel, which was discovered to be corrupt), thereby demoting it to an R3. Fortunately, by making two alterations (Blue spare from midpoint to 3pt, White spare from 9pt to 6pt) -- see diagram below, I was able to restore R4 integrity.

.....#1...Double 3s Position





White is Player 2

score: 0
pip: 127
Unlimited Game
Jacoby Beaver
pip: 143
score: 0

Blue is Player 1
XGID=-aACaBD------B-bbb-c--bbC-:0:0:1:33:0:0:3:0:10

Blue to play 33

Rollouts and additional information for the above R4 can be found here. (BTW, the links within that post may no longer be working.)

Later, I manufactured a second R4, the rollouts for which can be seen here. For reference, the position is also diagrammed below. (The Nactations for the retro-sequence have been updated.)

.....#2...Blitzy Board Position





White is Player 2

score: 0
pip: 155
Unlimited Game
Jacoby Beaver
pip: 147
score: 0

Blue is Player 1
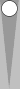XGID=-aBaBaB-B-Bb-C--aabbbb--B-:0:0:1:11:0:0:3:0:10
65R-64P-21D-33S-32@-52Z-43H-53Z-51H-43U-
64H-64R-61Z-31P-31D-65R-42D-43H-11Y-64S-
43H-F-64R-31U-54P-21H-51K-11e-53-11

Recently, I constructed a third R4 (diagrammed below), the rollouts for which can be seen here.

.....#3...Prime-versus-Prime Position





White is Player 2

score: 0
pip: 119
Unlimited Game
Jacoby Beaver
pip: 150
score: 0

Blue is Player 1
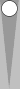XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:0:0:3:0:10

32S-43H-22E-22E-54@-44S-41U-51r-52R-11B-31P-32N-31D-65S-
F-66D-63H-F-11D-426-63r-21K-53-11A.-21-54J-528-21U-11


Timothy Chow suggested a scoring system for four-score positions, based on the size of margins (the higher, the better). You can follow our discussion in the thread that starts here and ends here.

I've further modified the system. Before summing the square routes of the margins at m, d, s and g, I award a compensating multiplier to the non-money margins:

.....sqrt m + sqrt 20d/9 + sqrt 10s/7 + sqrt 10g/7 = SCORE

Plugging the 3-ply rollout margins into this formula, let's score the three four-score positions discovered thus far:

.....Position with double 3s: ..sqrt 13 + sqrt 16*20/9 + sqrt 35*10/7 + sqrt 39*10/7 = 24.10
.....Blitzy board, double 1s: ..sqrt 32 + sqrt 15*20/9 + sqrt 48*10/7 + sqrt 33*10/7 = 26.58
.....Prime-v-prime double 1s: .sqrt 23 + sqrt 11*20/9 + sqrt 8*10/7 + sqrt 13*10/7 = 17.43

By that measure, my most recent effort ranks third. However, I was after a bonus feature that is not achieved in the first two poaitions. In the third position, there is a FIFTH play that rolls out best at a couple of scores (–2–4, and c–3). That play is E (Each) = 24/23 14/13 4/3*(2). Let's start by looking at the 3-ply rollout below.

.....–2–4 rollout with 3-ply checker, XGR cube





White is Player 2

score: 0
pip: 119
4 point match
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:0:4:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: -0.219
Player:
Opponent:		52.19% (G:12.97% B:1.47%)
47.81% (G:15.30% B:1.74%)		Conf.: ± 0.003 (-0.222...-0.217) - [90.0%]
Duration: 8 hours 38 minutes
2.Rollout124/23 8/7 4/3*(2) eq: -0.222 (-0.003)
Player:
Opponent:		52.23% (G:13.76% B:1.65%)
47.77% (G:13.91% B:1.91%)		Conf.: ± 0.003 (-0.225...-0.219) - [10.0%]
Duration: 8 hours 10 minutes
3.Rollout224/23 14/13 8/6eq: -0.229 (-0.010)
Player:
Opponent:		51.65% (G:11.71% B:1.01%)
48.35% (G:14.07% B:2.26%)		Conf.: ± 0.005 (-0.234...-0.224) - [0.0%]
Duration: 2 hours 16 minutes
4.Rollout224/23 12/11 4/3*(2) eq: -0.236 (-0.017)
Player:
Opponent:		53.13% (G:12.41% B:1.45%)
46.87% (G:16.82% B:5.94%)		Conf.: ± 0.007 (-0.243...-0.229) - [0.0%]
Duration: 1 hour 43 minutes
5.Rollout324/23 13/12 8/6eq: -0.253 (-0.034)
Player:
Opponent:		50.16% (G:11.25% B:0.93%)
49.84% (G:14.42% B:2.12%)		Conf.: ± 0.007 (-0.261...-0.246) - [0.0%]
Duration: 1 hour 15 minutes
1 41472 Games rolled with Variance Reduction.
Dice Seed: 15098271
Moves: 3-ply, cube decisions: XG Roller

2 10368 Games rolled with Variance Reduction.
Dice Seed: 15098271
Moves: 3-ply, cube decisions: XG Roller

3 5184 Games rolled with Variance Reduction.
Dice Seed: 15098271
Moves: 3-ply, cube decisions: XG Roller


So close. Next, I tried a 4-ply rollout, which is shown below:

.....–2–4 rollout with 4-ply checker, 4-ply cube (just 5k)





White is Player 2

score: 0
pip: 119
4 point match
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:0:4:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: -0.177
Player:
Opponent:		51.91% (G:12.39% B:1.52%)
48.09% (G:14.33% B:3.04%)		Conf.: ± 0.006 (-0.183...-0.171) - [100.0%]
Duration: 20 hours 21 minutes
2.Rollout124/23 14/13 8/6eq: -0.225 (-0.048)
Player:
Opponent:		51.52% (G:11.50% B:1.01%)
48.48% (G:13.88% B:2.13%)		Conf.: ± 0.005 (-0.231...-0.220) - [0.0%]
Duration: 14 hours 59 minutes
3.Rollout124/23 8/7 4/3*(2) eq: -0.228 (-0.051)
Player:
Opponent:		51.63% (G:13.83% B:1.64%)
48.37% (G:13.62% B:1.66%)		Conf.: ± 0.006 (-0.234...-0.222) - [0.0%]
Duration: 16 hours 34 minutes
1 5184 Games rolled with Variance Reduction.
Dice Seed: 85576101
Moves and cube decisions: 4-ply
Search interval: Large

Wow, that's a huge difference. This time, the E play wins by a mile!

Something is obviously amiss. I tracked the problem down to White's cube action. On the evaluation of 3-ply, XGR, XGR+ or XGR++, White correctly does not double the E play. However, on 4-ply eval White does double E, which (according to 3-ply rollout) is a mistake of .044. If we adjust for this mistake, E beats the other two plays by only .007 and .004.

However, instead of relying on this method of reconciliation and extending the 4-ply rollout (beyond its mere 5k), I decided to roll out (a) 4-ply checker with XGR cube, and (b) 4-ply checker with XGR+ cube. The results are shown below.

.....–2–4 rollout with 4-ply checker, XGR cube





White is Player 2

score: 0
pip: 119
4 point match
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:0:4:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: -0.215
Player:
Opponent:		52.14% (G:13.48% B:1.69%)
47.86% (G:15.35% B:1.79%)		Conf.: ± 0.002 (-0.217...-0.213) - [100.0%]
Duration: 3 days 04 hours 20 minutes
2.Rollout124/23 8/7 4/3*(2) eq: -0.222 (-0.007)
Player:
Opponent:		51.90% (G:13.72% B:1.73%)
48.10% (G:13.70% B:1.95%)		Conf.: ± 0.002 (-0.224...-0.220) - [0.0%]
Duration: 3 days 06 hours 43 minutes
3.Rollout224/23 14/13 8/6eq: -0.227 (-0.012)
Player:
Opponent:		51.51% (G:11.62% B:0.95%)
48.49% (G:13.82% B:2.10%)		Conf.: ± 0.004 (-0.231...-0.223) - [0.0%]
Duration: 18 hours 14 minutes
1 46656 Games rolled with Variance Reduction.
Dice Seed: 60580582
Moves: 4-ply, cube decisions: XG Roller

2 10368 Games rolled with Variance Reduction.
Dice Seed: 60580582
Moves: 4-ply, cube decisions: XG Roller

.....–2–4 rollout with 4-ply checker, XGR+ cube (just 5k)





White is Player 2

score: 0
pip: 119
4 point match
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:0:4:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: -0.215
Player:
Opponent:		52.14% (G:13.41% B:1.64%)
47.86% (G:15.19% B:1.77%)		Conf.: ± 0.005 (-0.220...-0.209) - [99.1%]
Duration: 15 hours 40 minutes
2.Rollout124/23 14/13 8/6eq: -0.224 (-0.009)
Player:
Opponent:		51.63% (G:11.97% B:1.08%)
48.37% (G:13.91% B:2.14%)		Conf.: ± 0.005 (-0.229...-0.219) - [0.8%]
Duration: 14 hours 40 minutes
3.Rollout124/23 8/7 4/3*(2) eq: -0.228 (-0.013)
Player:
Opponent:		51.70% (G:13.92% B:1.77%)
48.30% (G:13.60% B:2.21%)		Conf.: ± 0.006 (-0.234...-0.222) - [0.1%]
Duration: 14 hours 59 minutes
1 5184 Games rolled with Variance Reduction.
Dice Seed: 56228937
Moves: 4-ply, cube decisions: XG Roller+

Ignoring both the 3-ply rollout (given that we have a higher-ply rollout of good length) and the (bogus) 4ply/4ply rollout, and instead just looking at the last two rollouts, E beats its strongest rival by .007 and .013, respectively. (Note that I am discounting the play that finishes second in the 5k rollout due to so few trials.)

If we weight-average the .007 margin of the long rollout with the .013 margin of the admittedly-higher-setting-but-mere-5k rollout, E wins by about .008.

I have not empirically compared margins at the –2–4 score with those of the main scores. I suspect that an appropriate "tied" cusp is somewhere between that of gammon save (.007) and money (.010). I think it's fair to say that at –2–4, E is clearly best, but there is not enough information to determine whether E is also better than "tied."

For now, I conclude that this position is either an R4+1 or an R4+T1. (Which? It's currently TCTC.) Either way, it's the first position of its kind created.

[There is no such thing as a T5 or R5. The number immediately following the T or R is the number of MAIN scores (m, d, s, g) that have a different best play, and that number is capped at four. Following the plus sign is the number of other plays that are best at at least one other score. For example, if play A is clearly best at m and g, play B is clearly best at d and s, play C is tied/best at -2-5, and play D is clearly best at -3-7, -3-8 and -3-9 (no extra credit for these second and third scores), then I would call such a relatively unimpressive position merely a T2+2, or more accurately an R2+1+T1.]

There is another score at which E seems to be best, which is c–3 (i.e., player is at Crawford, opponent needs 3). See rollouts below.

.....c–3 rollout with 3-ply checker, XGR cube





White is Player 2

score: 0
pip: 119
3 point match
Crawford
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:1:3:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: +0.046
Player:
Opponent:		53.69% (G:13.31% B:1.63%)
46.31% (G:19.06% B:0.88%)		Conf.: ± 0.001 (+0.045...+0.048) - [99.9%]
Duration: 7 hours 58 minutes
2.Rollout124/23 8/7 4/3*(2) eq: +0.043 (-0.003)
Player:
Opponent:		53.64% (G:14.42% B:1.78%)
46.36% (G:17.98% B:1.03%)		Conf.: ± 0.002 (+0.041...+0.044) - [0.1%]
Duration: 7 hours 37 minutes
3.Rollout224/23 14/13 8/6eq: +0.038 (-0.008)
Player:
Opponent:		53.27% (G:11.05% B:1.02%)
46.73% (G:18.24% B:0.88%)		Conf.: ± 0.002 (+0.036...+0.041) - [0.0%]
Duration: 4 hours 52 minutes
4.Rollout224/23 12/11 4/3*(2) eq: +0.036 (-0.011)
Player:
Opponent:		54.47% (G:13.38% B:1.58%)
45.53% (G:20.65% B:2.13%)		Conf.: ± 0.002 (+0.033...+0.038) - [0.0%]
Duration: 4 hours 25 minutes
5.Rollout224/23 12/11(2) 8/7eq: +0.029 (-0.017)
Player:
Opponent:		53.09% (G:10.93% B:1.03%)
46.91% (G:21.16% B:1.08%)		Conf.: ± 0.002 (+0.027...+0.031) - [0.0%]
Duration: 4 hours 43 minutes
6.Rollout224/23 8/5eq: +0.028 (-0.018)
Player:
Opponent:		53.02% (G:10.72% B:0.89%)
46.98% (G:21.12% B:1.06%)		Conf.: ± 0.002 (+0.026...+0.030) - [0.0%]
Duration: 4 hours 38 minutes
7.Rollout312/8eq: +0.023 (-0.023)
Player:
Opponent:		54.94% (G:11.97% B:1.23%)
45.06% (G:27.34% B:3.03%)		Conf.: ± 0.004 (+0.019...+0.027) - [0.0%]
Duration: 1 hour 18 minutes
1 20736 Games rolled with Variance Reduction.
Dice Seed: 85576101
Moves: 3-ply, cube decisions: XG Roller

2 10368 Games rolled with Variance Reduction.
Dice Seed: 85576101
Moves: 3-ply, cube decisions: XG Roller

3 5184 Games rolled with Variance Reduction.
Dice Seed: 85576101
Moves: 3-ply, cube decisions: XG Roller

.....c–3 rollout with 4-ply checker, 4-ply cube (just 5k)





White is Player 2

score: 0
pip: 119
3 point match
Crawford
pip: 150
score: 2

Blue is Player 1
XGID=--aaBBBBA---BAA-aacbbbbAA-:0:0:1:11:2:0:1:3:10
Blue to play 11

1.Rollout124/23 14/13 4/3*(2) eq: +0.048
Player:
Opponent:		53.82% (G:12.87% B:1.67%)
46.18% (G:19.17% B:0.91%)		Conf.: ± 0.002 (+0.046...+0.050) - [59.0%]
Duration: 1 day 08 hours 48 minutes
2.Rollout224/23 8/7 4/3*(2) eq: +0.048 (0.000)
Player:
Opponent:		53.84% (G:14.21% B:1.74%)
46.16% (G:18.02% B:0.97%)		Conf.: ± 0.002 (+0.046...+0.050) - [41.0%]
Duration: 1 day 06 hours 22 minutes
3.Rollout324/23 14/13 8/6eq: +0.042 (-0.006)
Player:
Opponent:		53.47% (G:11.18% B:1.08%)
46.53% (G:18.23% B:0.88%)		Conf.: ± 0.002 (+0.040...+0.045) - [0.0%]
Duration: 1 day 04 hours 53 minutes
1 5467 Games rolled with Variance Reduction.
Dice Seed: 4254295
Moves and cube decisions: 4-ply
Search interval: Large

2 5466 Games rolled with Variance Reduction.
Dice Seed: 4254295
Moves and cube decisions: 4-ply
Search interval: Large

3 5184 Games rolled with Variance Reduction.
Dice Seed: 4254295
Moves and cube decisions: 4-ply
Search interval: Large

The existence of this additional E-supportive score does not further raise the four-score position's status, but note there is a sixth play in the fray. The closeness of margin suggests a slim but non-trivial chance that future rollouts could overturn and put F (Field) = 24/23 14/13 8/6 barely on top at the c–3 score. In such an event, the position status will be further lifted to R4+1+T1 or R4+T2.

Nack

Messages In This Thread

 

Post Response
Your Name:
Your E-Mail Address:
Subject:
Message:

If necessary, enter your password below:

Password:
 

 

[ View Thread ] [ Post Response ] [ Return to Index ] [ Read Prev Msg ] [ Read Next Msg ]

BGonline.org Forums is maintained by Stick with WebBBS 5.12.