I've been meaning to post more examples of XG's new rollout statistics feature but other priorities keep intruding. Here is an example that was suggested to me a while back by BGO reader AP. It's a position that Stick discussed in his 28 February 2010 Gammon Village article on "Two Away Four Away."
                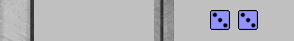                  |
| ||||
| XGID=-a----EaC---dEa--c-e----B-:0:0:1:33:2:0:0:4:10 | |||||
| Blue to play 33 | |||||
| 1. | Rollout1 | 24/21(2) 6/3(2) | eq: -0.076 | |||
| ||||||
| 2. | Rollout1 | 24/21(2) 13/10(2) | eq: -0.089 (-0.013) | |||
| ||||||
| 3. | Rollout1 | 13/7*(2) | eq: -0.118 (-0.042) | |||
| ||||||
| 1 46656 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller | ||||||
eXtreme Gammon Version: 2.19.208.pre-release, MET: Kazaross XG2
The rollout puts the money-game play of 13/7*(2) well behind the anchor-advancing plays. But notice this: if you look at the pseudocubeless win and gammon numbers you may be puzzled because 13/7*(2) seems to win enough extra games and gammons to compensate for the extra gammon losses, given that Blue's gammon value with a centered cube is (nearly) 1. However, as Stick correctly noted in his article, the problem is that the cube gets turned a lot at this score. Unfortunately, using only traditional bot information, there is no way to find out just how often the cube gets turned.
Using GNU's "View Statistics" XG's "rollout statistics," however, we can get a quantitative answer. The table below (where I've included rollout statistics for plays 1 and 3) shows that Blue wins an undoubled gammon (or backgammon) only (2793+835)/46656 or about 8% of the time. The rest of the time, the gammon win is meaningless.
XGID=-a----EaC---dEa--c-e----B-:0:0:1:33:2:0:0:4:10
24/21(2) 6/3(2) Non VR Equity: -0.074 (Cost: +69.90%)
Cube Win BG Win G Win S Cash Pass Lose S Lose G Lose BG D/T D/P Take % D/T D/P Take %
1 318 2,454 15 9,830 8,526 23 158 6 2,534 9,830 20.49% 22,792 8,526 72.78%
2 213 1,967 6,537 25 11,745 2,104 233 2,502 25 99.01%
4 11 180 1,823 464 21 3
XGID=-a----EaC---dEa--c-e----B-:0:0:1:33:2:0:0:4:10
13/7*(2) Non VR Equity: -0.101 (Cost: +69.61%)
Cube Win BG Win G Win S Cash Pass Lose S Lose G Lose BG D/T D/P Take % D/T D/P Take %
1 835 2,793 5 7,496 7,787 6 117 2 2,080 7,496 21.72% 25,535 7,787 76.63%
2 460 3,462 7,238 8 10,357 3,591 429 2,070 8 99.62%
4 20 221 1,425 374 28 2
A more accurate way to compare 24/21(2) 6/3(2) and 13/7*(2) is as follows (ignoring undoubled backgammon losses):
24/21(2) 6/3(2):
Wins 1 point: 21.1% (ME = 81%)
Wins 2 points: 28.9% (ME = 100%)
Loses 1 point: 18.3% (ME = 60%)
Loses 2 points: 25.6% (ME = 50%)
Loses 4 points: 6.1% (ME = 0%)
Overall MWC: 69.8%
13/7*(2):
Wins 1 point: 16.1% (ME = 81%)
Wins 2 points: 35.3% (ME = 100%)
Loses 1 point: 16.7% (ME = 60%)
Loses 2 points: 22.5% (ME = 50%)
Loses 4 points: 9.5% (ME = 0%)
Overall MWC: 69.6%
From this we can see that although 13/7*(2) wins more often and also wins 2 points more often, it also loses 4 points more often, which is a huge minus.
This way of looking at match-play decisions undoubtedly seems difficult to understand, but I believe that it's mostly because the approach is unfamiliar, not because it's any more difficult intrinsically. The big advantage is that the calculations are actually correct. There is no muddling of the distinction between cubeless gammons and actual gammons, nor is recube vig bundled up in a mysterious approximate number that comes out of nowhere.
There is still room for figuring out the right concepts (analogous to gammon values and recube vig) to make this kind of analysis usable for OTB estimates in practical play. I don't claim to have solved that problem yet. But the first step, I believe, is to focus on the correct numbers and try to find a way to learn what they are telling us, rather than keep muddling along with black-magic adjustments to incorrect numbers just because "it's always been done that way before."