BGonline.org Forums

Problem: Cube action? - RO and a Challenge

Posted By: Daniel Murphy
Date: Tuesday, 18 September 2012, at 12:08 a.m.

In Response To: Problem: Cube action? (Daniel Murphy)

First, the challenge: find a position

• in an unlimited match
• with contact
• where correct cube action is double/take, and
• the favorite's equity after double/take is less than 0.120

Lowest possible equity after correct double/take was the topic of an r.g.bg discussion in 2006. I think this position (below) is better than any suggested then.

Second, the position. Double/take and redouble/take:

Unlimited match, Blue on roll.

White	37
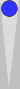Blue	88
Position ID: /X4EAIBtuwGAAg Match ID: cAkAAAAAAAAA

Cube decision
Rollout cubeless equity		+0.0498
Cubeful equities:
1.	Double, take	+0.1204
2.	Double, pass	+1.0000	+0.8796
3.	No double	+0.1111	-0.0093
Proper cube action:		Double, take
Rollout details
Win W g W bg Lose L g L bg Cubeless Cubeful Centered 1-cube 0.5260 0.0000 0.0000 - 0.4740 0.0022 0.0000 +0.0498 +0.1111 Standard error 0.0000 0.0000 0.0000 - 0.0000 0.0000 0.0000 0.0001 0.0000 Player White owns 2-cube 0.5377 0.0000 0.0000 - 0.4623 0.0018 0.0000 +0.1472 +0.1204 Standard error 0.0002 0.0000 0.0000 - 0.0002 0.0000 0.0000 0.0009 0.0011
Full cubeful rollout with var.redn.
7776 games, Mersenne Twister dice gen. with seed 695348782 and quasi-random dice
Play: world class 2-ply cubeful prune [world class]
keep the first 0 0-ply moves and up to 8 more moves within equity 0.16
Skip pruning for 1-ply moves.
Cube: 2-ply cubeful prune [world class]

White	37
Blue	88
Position ID: /X4EAIBtuwGAAg Match ID: UQkAAAAAAAAA

Cube decision
Rollout cubeless equity		+0.0488
Cubeful equities:
1.	Double, take	+0.1204
2.	Double, pass	+1.0000	+0.8796
3.	No double	+0.1178	-0.0026
Proper cube action:		Redouble, take
Rollout details
Win W g W bg Lose L g L bg Cubeless Cubeful Player Blue owns 2-cube 0.5255 0.0000 0.0000 - 0.4745 0.0023 0.0000 +0.0488 +0.1178 Standard error 0.0001 0.0000 0.0000 - 0.0001 0.0000 0.0000 0.0001 0.0001 Player White owns 4-cube 0.5377 0.0000 0.0000 - 0.4623 0.0018 0.0000 +0.1472 +0.1204 Standard error 0.0002 0.0000 0.0000 - 0.0002 0.0000 0.0000 0.0009 0.0011
Full cubeful rollout with var.redn.
7776 games, Mersenne Twister dice gen. with seed 695348782 and quasi-random dice
Play: world class 2-ply cubeful prune [world class]
keep the first 0 0-ply moves and up to 8 more moves within equity 0.16
Skip pruning for 1-ply moves.
Cube: 2-ply cubeful prune [world class]

Some observations:

(1) I don't know why rollout ND cubeful equity with centered cube is reported as 0.111. It should be ever so slightly lower because of gammons. After some of Blue's nonhitting rolls, White is very slightly too good to double, Gnubg evaluations recognize that, so White should be winning a handful of gammons in the rollout of the original position.

(2) When Blue doesn't hit, he loses nearly 100% of the time. He never wins the race with a centered cube or if White has the cube, because he gets doubled out first. After not hitting, Blue's only victories come from very rare sequences: Blue misses and runs with only 1 checker, White (who is very slightly too good to double) rolls 1-1, Blue fans, White takes 6 checkers off the 3 point while Blue fans once or twice more and then hits. If Blue owns a 2-cube, doesn't double, and rolls 6-6 he wins about 4% cubeless; 5-5 about about 2.5% cubeless; 6-5 about 0.5% cubeless; 4-3 about 0.3%.

(3) Blue hardly ever gets gammoned. The probability is less than 0.2%.

(5) Since all aces and deuces hit, Blue must run with all hitting numbers unless he breaks his board. Breaking the board is not a good play. Blue should run with both checkers sometimes, maybe all the time -- some extra rollouts say running both checkers is best with 3-4 and also with 3-3, but wrong by less than 0.001 with 3-5. Since Blue always runs at least one checker, White never leaves a shot next turn, and Blue's chance of ever getting a second shot is remote (starting with White rolling 1-1, as described above).

(6) After doubling or redoubling and a hit, Blue wins about 96% of the time, that is, he wins 96% of 55.55% = 53.33% (in a rollout of Blue's winning chances after redouble/take and 52: 21/19*/14, Blue won 95.75% of all games, cubeful).

(7) If we ignore racing wins, gammon losses and redoubels, the math is:

ND -> 0.555 - 0.444 = 0.111 * 1 = 0.111

DT -> 0.533 - 0.467 = 0.066 * 2 = 0.132

With 0.2% gammon losses:

ND -> 0.555 - 0.446 = 0.109 * 1 = 0.109

DT -> 0.533 - 0.469 = 0.064 * 2 = 0.128

Messages In This Thread

• Problem: Cube action?
  Daniel Murphy -- Saturday, 15 September 2012, at 4:51 a.m.
  • Problem: Cube action?
    Taper_Mike -- Saturday, 15 September 2012, at 5:41 a.m.
    • Problem: Cube action?
      Timothy Chow -- Saturday, 15 September 2012, at 6:12 p.m.
  • Problem: Cube action?
    Snua -- Saturday, 15 September 2012, at 1:00 p.m.
  • Problem: Cube action?
    Igor -- Saturday, 15 September 2012, at 5:32 p.m.
  • Problem: Cube action?
    benf -- Saturday, 15 September 2012, at 6:46 p.m.
  • Problem: Cube action?
    Martin -- Sunday, 16 September 2012, at 8:24 a.m.
  • Problem: Cube action?
    Chuck Bower -- Sunday, 16 September 2012, at 2:50 p.m.
  • Problem: Cube action?
    ah_clem -- Monday, 17 September 2012, at 5:36 p.m.
  • Problem: Cube action? - RO and a Challenge
    Daniel Murphy -- Tuesday, 18 September 2012, at 12:08 a.m.
    • Problem: Cube action? - RO and a Challenge
      Daniel Murphy -- Wednesday, 19 September 2012, at 5:32 p.m.