       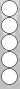                           |
| ||||
| XGID=-b-B--E-C---eD---c-e----A-:0:0:1:00:0:0:3:0:10 | |||||
Each side played twice | |||||
From the standard opening position, each side (legally) moved twice. How is this possible?
Congratulations to Bob Koca (by e-mail), Brian Lonergan (by e-mail) and Casper (by post) for solving the Three-point Mystery!
First, contemplate how Blue gets from his starting position (167 pips) to his target position (136 pips). More specifically, he will have net played 24/3 (21 pips) and 13/3 (10 pips), which requires six crossovers.
Either Blue is hit or he is not. If he IS hit, (at least) a seventh crossover is required, in which case both his rolls must be doublets, and he will have a checker on the bar when he rolls his second doublet. Based on the final position, his bar checker must reach either reach his 3pt or replenish his 13pt, 8pt or 6pt, and there is no roll that accomplishes that (as White's 6pt and 8pt block 66 33 44). Therefore, Blue was NOT hit.
As Blue was not hit, the total of Blue's two rolls is simply 167 – 136 = 31 pips, which clearly means that one roll is a non-doublet (as the total is indivisible by 4) and the other is larger than 44. The two possible breakdowns are: (a) 55 plus 65, or (b) 66 plus a 7-pip roll.
We can further narrow (b), because 24/3 is 21 pips and 13/3 is 10 pips (see first paragraph). If we remove three 6s from the 21, and one 6 from the 10, what is left over is a 3 and a 4. In short, Blue's two rolls are either: (a) 55 + 65, or (b) 66 + 43 [without yet addressing which order the rolls occurred].
You may well find it easier to solve the problem by visual trial and error (I would, very much so), but if you find yourself visually or imaginationally "blocked," this sort of deduction is available as an aid, for at least part of the solving process.
The (a) possibility of 55 + 65 is easier of the two to see, because of the way those rolls are typically played in the early game of backgammon. However, you'll expand your horizon (even if it doesn't help for this specific problem) if you realize that 24/13 and 13/3(2) (in one order or the other) is not the only way with 65 and 55 to get from the opening position to the target position. Blue doesn't have to play 24/13. Instead, he can play S (Split, 24/18 13/8) or even C (Cross, 24/18 8/3), and you'll transpose after playing the subsequent 55 roll. [Further, imagine White's 6pt did not exist. In that case, Blue could roll 55 first, and instead of 13/8(2), he might instead play 24/19 13/8 13/3 or 24/19 13/3 8/3 or 24/14 13/3 or 24/14 8/3(2) or 24/9 13/8 or 24/9 8/3!]
Counting backwards from the newly featured point (in this case, Blue's 3pt) can sometimes alert you to such possibilities. For 65 and 55 (in either order), I'll leave this as an exercise for the reader.
Let's try it for (b) 66 + 43. If we move the 6s backwards, what happens? (Do not automatically move doublets in pairs -- this is exactly the warning we so often hammer into beginners when they're playing moves in backgammon games.) If we backwardly play one checker 3pt to 9pt and the other 3pt to 21pt, does that look like anything? You bet! It looks exactly like Blue has played opening 43Z (reverse split, 24/21 13/9).
How does it work instead to first move 43 backwards? Backwardly play 3pt to 7pt with a 4, and 3pt to 6pt with a 3 -- that's the 43 roll. Then, for the 66, 7pt to 13pt and 6pt to 24pt returns you to the opening position, except for the fact that White's 6pt blocks that possibility. [Note that five paragraphs ago, you used a relieable method to determine that Blue's 7-pip roll must be 43. Had you not done so, you could here try moving 52 backwards, then 61 backwards, and you'll quickly see that in both cases the backwards 6s do not then go to the right spots.] Thus, going forwards, the 43 must be rolled before the 66.
In short, Blue reaches his side of the position with (a1) 65 + 55, (a2) 55 + 65, or (b) 43Z + 66P.
       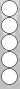                           |
| ||||
| XGID=-b-B--E-C---eD---c-e----A-:0:0:1:00:0:0:3:0:10 | |||||
Each side played twice | |||||
White finishes with the same position she started with; that is, she nets zero pips. Obviously, that can happen only if she is hit (at least once) and the pip total of her rolls is exactly the same as the total pips she is sent back when she is hit.
Naively, one might think that White can split off her 24pt, get hit and simply remake it with bar/24. However, one can't roll an ace by itself. Therefore, recycling the 24pt checker alone doesn't work. White must move off a checker(s) off some other point and replenish it.
The next lowest point is the 13pt (midpoint). Can White move a 13pt checker, have it hit and play bar/13? Well, a roll of 33 would do just that, except that Blue's 6pt is inconveniently blocking bar/13. Therefore, White must use a 24pt checker to replenish the midpoint. This can be achieved if White uses her part of her first roll to get a 24pt checker in direct range of the 13pt (i.e., to the 18pt, 16pt or 15pt), while simultaneously moving a checker off the 13pt (so it can be hit). In that way, on her second turn, White can roll 1x, where the "x" moves the 24pt-sourced checker the rest of the way to the 13pt.
We determined earlier that the only points on the far side of the board that Blue can "tag" along the way are White's 4pt, 7pt or 10pt (via 43Z, 65R or 43Z+6, respectively). White needs to slot/start one of these points first. Obeying the conditions clarified in the previous paragraph, White's dovetailing plays are 63S (Split, 24/18 13/10), 33S (3:1 Split, 24/15 13/10), and 33b (Both, 24/18 13/7).
There is a "catch 22" involving Blue's (a1) 65 + 55 and (a2) 55 + 65 combinations. If Blue rolls 65 before 55, White must slot her 7pt first (so as to get hit there), but her only qualifying play is 33b, and an opening doublet is illegal. On the other hand, if Blue rolls 55 before 65, he cannot have an opening doublet so White must have the opening roll, but again White cannot open with 33b.
That means, assuming there is a solution at all, Blue's play combination must be (b) 43Z + 66P, and the point on which he hits must be White's 10pt (as White cannot slot her 4pt while simultaneously moving a back checker into direct range of her 13pt).
Obviously, White must enter and replenish the midpoint on the second of her two turns. She cannot enter until she gets hit, and she cannot hit before she has left a blot. And, as Blue and White must alterate turns, it can only happen this way: Blue opens with 43Z, White starts the 10pt, Blue hits there, White enters.
Specifically, these two (very similar) sequences work:
.....(1) 43Z, 63S (24/18 13/10), 663 (21/15*/3 9/3), 51R (bar/24 18/13)
.....(2) 43Z, 33b (24/15 13/10), 663 (21/15*/3 9/3), 21R (bar/24 15/13)
Below, for sequence #1, is the key diagram after 43Z-63S. I'll trust you can visualize the rest:
                                  |
| ||||
| XGID=-a----EaCA--dD-a-c-e-A--A-:0:0:1:66:0:0:3:0:10 | |||||
Blue played 43Z, and White played 63S | |||||
In the alternate sequence (#2), White played 33b instead of 63S.
(To create the alternate diagram, move her 18pt checker to the 15pt).
Nack