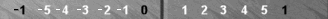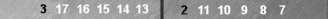For reference, this diagram is repeated from post #3. Please note the similarity between White's formation below and Blue's formation in the third diagram here.
| Six-sym around the -2pt | |
|---|---|
| |
Could you clarify the Symmetry in White's inner board, please? You seem to use the 1st man on the six point as part of the symmetrical pattern, while at the same time saying it counts zero because it's on S0. I can't see how it logically can count zero and also be used as part of a cluster, which implicitly makes it a contributor to part of a non-zero count.
This zero-count checker does indeed contribute to a non-zero count. However, its contribution is only as a visual aid; otherwise its existence is irrelevant.
The beauty of the 0pt (trad 6pt) checkers is that you can use them or not in a count, as convenient. Most of the time, it is best to remove/ignore all of them. But it can sometimes help to retain or even manufacture one (or more); neither alters the count. (Secrets of the modern universe: n0 is both a black hole and a white hole.)
Here, again, is White's complete near side position:
| -2(+1) | |
|---|---|
| |
As you know, you can remove the four 0pt checkers without altering the count:
| -2(+1) | |
|---|---|
| |
| -2 | |
|---|---|
| |
There are two aspects to be aware of, however:
(1) The distance between the most polarized checkers of the formation is 6 pips; it is a little easier to spot symmetry when they are closer together.
(2) The bar buffers the n1 checker from the rest of the formation. That can be an impediment to perceiving symmetry clearly, especially on these diagrams where the bar is so wide (though, as with any counting system, bar distortion becomes much less noticeable as you practice with that system).
For those reasons, many people would find it easier/clearer to make this one-pip shift instead:
| -2 | |
|---|---|
| |
If you like (having accounted for the 1-pip adjustment and working from the diagram above), you can remove the 0pt checker, like this:
| -2 +13 = -11 | |
|---|---|
| |
This five-checker formation happens to be a "tandem," because from White's perspective it looks like the top of a tandem bicycle with the blot being the handle bars and the points being the two riders. In White's own inner board location and facing this direction her tandem counts -2.
I put another tandem (bicycle) on the side of the board facing us so that you can see it right-side up. Here, the tandem counts 13 (15 more than -2, because it is a five-checker squad three quadrants away). By an eerie coincidence, if you shift White's back checker points outward a pip, you get the 13-count formation that exists in Jim's original position.
But I'm just having fun now; complex squads will come much later, if you need/want to learn them at all. The main point is that the six-sym (shown in the previous diagram) is a basic count, whereas the tandem (shown just above), even though it uses one fewer checker, is an advanced count. Hence, having that checker on the 0pt proves useful even though it contributes zero to the count.
Back to the original formation before the 1 pip was moved:
| -2(+1) | |
|---|---|
| |
It comes to the same thing, except when possible I slightly prefer (b), which counts extra pip(s) in the outer board last rather than (a), which requires accounting for pip movement(s) before the complete supe count has been obtained. (If you don't follow this part, it's okay -- it's an unimportant detail.)
Nack