                                  |
| ||||
| XGID=--b-CBCBD----A-a--bbbbbb--:0:0:1:00:0:0:3:0:10 | |||||
Reach this position in nine rolls (with a condition) | |||||
Part 1 of this puzzle was posted here. Part 2 was posted here (in this thread). I'm reiterating Part 2's objective in the next paragraph.
Objective: To get from the opening position to the above position legally in nine rolls (five for one player and four for the other), with this condition added: Each time Blue moves a checker off the 24pt, it must play the entire roll by itself.
Descriptive Solution:
Firstly, could it have been White that rolled only four times? Let's check.
From an opening pipcount of 167 to her current pipcount of 110, White has advanced 57 pips. That's an odd number, which means that one of White's rolls had to be a non-doublet. If we grant her doublets for her other three rolls, she has moved 2 + 4 + 4 + 4 = 14 "portions" (sub-moves). Is that enough?
No. At a minimum, White requires three portions for her 6pt spares, three for her 8pt checkers, and at least seven portions for her midpoint checkers (five to come down and two to jump the bar), and two portions for 24/23(2). That's a total of 15 portions, one more than the 14 that can be played by one non-doublet plus three doublets. White must have been the player to roll FIVE times.
Thus, we know that Blue rolled only four times. At a minimum, he needs four portions for his midpoint checkers, five for the checkers moved to his 5pt and 4pt, and six to get his 24pt checkers to the 8pt or lower. That's (at least) 15 portions. Therefore, all four of Blue's rolls must be doublets (using 16 portions).
Having reduced his opening pipcount of 167 to his current count of 99, Blue's four doublets total 68 pips. We know that one of his doublets must be either 66 or 11, to make the 7pt. We know that Blue needs either 22 or 11 to take the spares off his 6pt. And we know that his back checkers escape with 55 55, 55 44 or 44 44, as they must go to one of the five points spanning his (8pt-to-4pt) prime.
There are only two Blue-roll combinations that meet the above criteria (including the 68-pip total). We can eliminate 66 55 55 11 because both 55s would be played 24/4, leaving no way to get a fourth checker to the 8pt. The only workable combination is 66 55 44 22, which means we know that (exactly) one back checker plays 24/8 with 44, and the other plays 24/4 with 55.
Wait a minute! Given that White's 6pt is occupied, how is it possible for Blue to escape a back checker with 55? Well, in the words of Conan Doyle's character Sherlock Holmes, "When you have eliminated the impossible, whatever remains, however improbable, must be the truth."
The inescapable conclusion is that White must completely vacate her 6pt (thereby allowing Blue to cleanly escape with 55) and then remake it!
There are several solutions, though all are similar. The one that Tim found is demonstrated in the series of four diagrams below (displayed left, right, left, right, if your window is wide enough).
       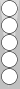                           |
| ||||
| XGID=-b----EDC---dA-a-b-e---aB-:0:0:1:00:0:0:3:0:10 | |||||
White played an opening 63, and Blue played 66 | |||||
       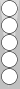  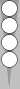                         |
| ||||
| XGID=-b--BBCBC----A-a-bde---aB-:0:0:1:00:0:0:3:0:10 | |||||
White played 66D, and Blue played 22A | |||||
         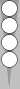                         |
| ||||
| XGID=-b--BBCBD----A-a-bdb-b-bA-:0:0:1:00:0:0:3:0:10 | |||||
White played 22I (Inside, 6/4(3) 4/2), and | |||||
                                  |
| ||||
| XGID=-b--CBCBD----A-a--d-bbbb--:0:0:1:00:0:0:3:0:10 | |||||
White played 33A (Attack, 8/5(2) 6/3(2), and | |||||
And here we are. As promised, White has vacated her 6pt, and Blue has escaped his 55 (moving all the way from his 24pt to his 4pt).
White now rolls 11 and snaps in place the last jigsaw puzzle piece by playing c (cross, 24/23(2) 7/6(2)), thereby reaching the final position that is diagrammed below (and at the beginning of this post).
                                  |
| ||||
| XGID=--b-CBCBD----A-a--bbbbbb--:0:0:1:00:0:0:3:0:10 | |||||
Final Position | |||||
How many solutions are there?
To find this out, one needs to figure out White's permutations, similarly to how we did with Blue earlier (except White's situation is a bit more complex). This post is already long enough, though, so I’ll cut to the chase. White has two roll combinations: 66 33 22 11 63, and 66 33 22 11 54, which must be played in one of the following orders:
........63 66 22 33 11 (Blue 44 second or third)
........63 66 33 22 11 (Blue 44 second)
........63 22 66 33 11 (Blue 44 third)
........54 66 33 11 22 (Blue 44 third)
........54 33 66 11 22 (Blue 44 third)
To the right of each permutation is some information about Blue (whose rolls, as deduced earlier, are 22 66 44 55 in some order). Blue's 44 must escape after White's midpoint is vacant but before White's 5pt is occupied (else 44 will be blocked or will hit); in other words, after 63 66 or 54 66 33, and before 33 in the upper (63) group or 11 in the lower (54) group.
White's 6pt is never vacant until just before her fifth (final) turn, so Blue can only exit with 55 on his fourth (final) turn.
The first of White’s five roll orders gives Blue two options for when to exit with 44, adding a sixth possible two-player roll order. That subtotal is doubled, however, as Blue's 66 and 22 are always interchangeable, giving us eight orders starting with 63, plus four starting with 54.
White's opening 54 can only be 13/8 6/2. However, her opening 63 can be either 13/10 13/7 or 13/10 8/2 (with her 66 being either 13/7(3) 8/2 or 13/7(4), respectively). That doubles the subset of eight, for a total of 16 + 4 = 20 distinct roll/move sequences.
[Twenty is actually a small number. Part 1 of this problem (i.e., without the 24pt-checker condition) has a much larger number. Even the relatively simple great prime problem, which is only three rolls (compared to this problem's nine), has twelve distinct roll/move sequence solutions (by my count).]
For reference, the penultimate position when White has opened with 54N and just before she has played her (final) 22, is shown below.
Nack
                                  |
| ||||
| XGID=--b-CBCBD----A-a-cb-babb--:0:0:-1:22:0:0:3:0:10 | |||||
White will remake her prime with A (Attack, 8/6(3) 6/4) | |||||