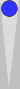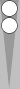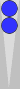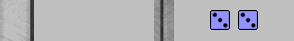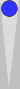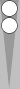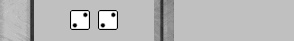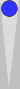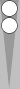Congratulations to Mike Clapasdle for his correct solution! (I'll provide a link to it later in this post.)
Puzzle: Starting from the diagram above, each player makes FOUR moves, there are NO HITS. One player, having had FOUR DIFFERENT ROLLS, ends up with BLOTS ON FIFTEEN CONSECUTIVE POINTS.
Here is my main solution:
In the puzzle's starting position (51S-21S) diagrammed above (though dice are not shown), Blue rolls double 4s.
It is the starting 44 roll that defines this solution. From this point, (a) all Blue's rolls and moves and their order, and (b) all four of White's rolls and their order, are unalterable. (There are, however, as you will see, two additional variants from White's alternate move-portion choices of 8/5 and 8/6).
With his 44, Blue played 24/20/16 13/9(2), beginning the process of extracting his checkers from the far side of the board. White is not allowed to hit or be hit (so Blue's 6/2 is likewise barred, temporarily), and therefore by the time the target position is reached, Blue must vacate all points higher than his own 9pt (his 10pt being White's 15pt, the rear point of White's intended 15-checker blot-prime). A second (more subtle) purpose for this 44 move was to set up an efficient 33 for Blue's next move.
White now has a roll of 33 (in the diagram above).
With her 33, White played 23/20 (so that she can escape that checker with a 5). A checker on White's 10pt is a vital ingredient of her blot-prime, and to get it there she can't afford to squander three precious aces (with 13/12/11/10); therefore, the second 3 is 13/10. After that, 6/3 must be a third 3 (as 8/5 is the only other one that doesn't overrun).
The fourth 3 was optional. [I chose (a second) 6/3 for White's fourth 3 instead of 8/5 for an unimportant reason: to maintain the suspense of whether White will later play a 5 to her 3pt or to her 1pt.] It is interesting that a second 13/10 was not a viable option: by committing an ace to 10/9 White will lose the ability to play 13/11/9 with two deuces next turn, and 8/6 6/4(3) and 8/4 6/4 3/1 are overruns (given the need to play a 5 in the same area); her only remaining choice is to put a checker on her 2pt, which she can't because Blue will still be there!
White's 33 had to be the first of her four rolls. She could not roll 22 (nor 55 nor 11, of course) prior to her 33, because Blue checkers are currently in the way. [IF her 9pt were vacant, White could have played 22 as 13/9 8/4 or 13/9 6/4(2). Or IF her 2pt were vacant she could have played 22 or 62 as 8/2 6/4. (Or with both 9pt and 2pt vacant, White would also have had the choice of 13/9 6/2.)]
Blue now has his own roll of 33 (in the diagram above).
With his 33, Blue played 16/13 6/3(3), progressing further on both sides of the board by making effective use of all four 3s. Once he thoroughly vacates his 6pt, Blue will afford White an ideal escape with 55. (If Blue had instead rolled another 44, he could have moved most of the checkers off the 6pt well enough, but his 16pt checker would have been stuck, leaving White no legitimate way to play 22.)
In his first two moves, Blue used two 4s and one 3 to creatively "lovers-leap" the 24pt checker to the 13pt. Note that he could not have played the 3 first (24/21) because White's 8pt would have blocked the 21/17/13 route for the 4s. That is, Blue's 44 had to precede his 33.
Blue could not have rolled 55 before 33 (i.e., order of 44 55 33...), because he would be unable to get all five checkers off the 6pt prior to the last moment White can play 55 (which must precede her 11 because Blue will use a different roll to vacate White's 9pt than he uses to vacate her 12pt -- each is married to only part of the 6pt clearance).
White now has a roll of 22 (naturally, as her 55 and 11 are still blocked) -- in the diagram above.
With three of her deuces, White played 13/9 6/4 (forced). With her fourth 2 she played 3/1 (though 8/6 was a fine alternative that will transpose as soon as White has played her spare 5 -- to either her 3pt or 1pt).
Blue now has a roll of 44 (in the diagram above).
With 44 (the second one in his roll set), Blue played 13/9(2) 6/2(2), just in time to (finally) unleash White's 55.
And that is precisely what White rolls -- 55 (in the diagram above).
With three of her 5s, White played 24/19/14 20/15. With her fourth 5, she played 8/3. At this juncture, she is just one step away from completing her blot-prime.
Blue now has a roll of what? You guessed it -- 55 (in the diagram above).
With his 55, Blue threaded the needle by playing 23/18 18/13 13/8(2). Without a roll portion to spare, he has succeeded at the extraction operation, though it's really a co-operation.
White now has a roll of 11 (in the diagram above).
White played 13/12 10/9 8/7 6/5, and it's time to take a picture. White's formation speaks for itself, but Blue's is far from random. If you draw a vertical line to the left of the 6pt, Blue's cluster of checkers on the right is a mirror image of his cluster on the left, except it is twice as tall.
Let us move from the specific to the general. For reference, below is a repeat of the starting diagram:
Puzzle: Each player makes FOUR moves, there are NO HITS. One player, having had FOUR DIFFERENT ROLLS, ends up with BLOTS ON FIFTEEN CONSECUTIVE POINTS. (You are not told who rolls first, or who will make the blot-prime.)
How does one go about solving this type of puzzle? One would like to minimize trial and error.
Bob Koca provided some helpful observations, which I've paraphrased (and renumbered) below.
(1) Blue has nine checkers on his lowest eight points. He is too advanced to create a full blot prime (unless he is hit/recycled, but a condition of the puzzle is that neither player is hit). Therefore, it must be White who makes the blot-prime.
(2) White will play at least thirteen roll portions (five from her 6pt, one from her 8pt, three from her 13pt, and four with her back checkers). This means that at least three of her four rolls are doublets. (Two doublets and two non-doublets would account for only twelve portions.)
(3) As two aces (13/12 and 8/7) are necessary, 11 is one of White's four rolls. (There cannot be two non-doublets each having an ace; it has been established that there is at most one non-doublet.)
(4) 66 is eliminated (White potentially has 24/18 23/17 8/2 but the fourth 6 would overrun her target blot-prime). Given that she moves 44 pips (calculated by subtracting her 120 finish from her 164 start) with no repeated roll permitted, and that 11 is one her rolls, we know the other three rolls total exactly 40 pips. Therefore, 55 must also be one of the rolls. (The total of the largest rivals, 44 33 65, is a pip shy of 40.)
Let's reason a bit further. If we subtract the 20 pips (of the double 5s) from 40, the remaining 20 pips must be the sum of the other two rolls. The possible combinations are 44 31, 33 53, 33 22, 33 62.
I will discuss (and eliminate) the 44 31 in the third-to-last paragraph of this post. For the 33 53, the absence of even numbers in the roll set saddles White with an impossible parody situation in her inner board. That leaves either 33 22 or 33 62 (to accompany the other two rolls of 11 55 already deduced), though 62 is really just a specific case of 22.
The roll set of 11 55 33 22 works for all solutions. 11 55 33 62 works in the subset of solutions where 8/2 is a viable way to play three deuces. In those subset cases, a second 13/10 is necessary for double 3s (so that an ace can later slot the 9pt where 13/9 is not played with two deuces). Indeed, Michael's solution employs a 62 scheme. [By the way, there are twenty-four slight variants of his expedient 24/21 + 55-escape theme -- eight different ways that various 33, 62/22 and 55 moves interact, and the final 44 can be 55 or 66. If an at-least-one-non-doublet condition is added, there are just three variants.]
It turns out to be unnecessary for Blue to break his 6pt. (I had based the problem on the sneaky idea that White is forced to play three 5s with her back checkers -- including 24/19 -- hallucinating that 8/3 and 6/1 could not both be played.) With the same roll set, White starts with 33, playing 24/21 23/20 13/10(2). Then with 55 she plays 21/16 20/15 8/3 6/1. Then with 22 she plays 16/14 6/4 6/2, and (as usual) 11 finishes. [Or 33 + 55 can be delayed and/or 22 can be anywhere in the order.] In the meantime, Blue can easily escape by his third turn -- e.g., 65@ + 55B + xxD (or wait until the fourth if he wishes), and squander the other roll. In fact, Blue doesn't even have to roll first. (With this approach, and with no other, White can roll first.)
I discovered the above resource only after my initial posting. Otherwise, I might have required at least one non-doublet between the players, greatly reducing the number of solutions (in particular, eliminating the easy end run around the 6pt). More likely, I would have switched back to the 51S-21U position I first intended (in which case 62 is nixed because a deuce must be spent on 13/11). The sequence (after 51S-21U) is 44E (out, make 2pt)-33I(down, slot, make 3pt)-33E.(run to mid, vacate 6pt)-55E(run, slot 1pt), and to finish off Blue gets 55 twice while White completes her blot-prime with 22 and 11. [Blue can play the first of his two 55s in three ways (trivial transpositions), and in two of those he can change his last roll to 66, and White's 55 and 22 can be reversed -- technically ten solutions but clearly a single theme. [Failing to look closely, I thought the 51S-21S position I chose to post also had a unique theme and with fewer than ten solutions.]
Returning to the featured 51S-21S position, there are several near misses with the roll set of 11 31 44 55, and even 11 11 44 55 (though the latter set is disqualified anyway by the different-roll condition). White can easily blot-prime in a vacuum, but with Blue's pieces on the board, the two sides can't quite slip past each other. White can play neither 55 nor 44 until Blue breaks his 6pt (with five 2s and/or 3s), and White's only other roll in the interim is 31 (or 11), where the only blot-prime-friendly choices either hit or block Blue's vital escape routes.
Typically, I aim to impose as few "conditions" on a puzzle as is reasonably possible, but this one is tricky. For example, if I had not required four different rolls for White, Blue can move his 8pt stack with 22 and whip around his back checkers, while White plays 33, 33, 44 and 11 (i.e., runs with six 3s plus 13/10 6/3, then 13/9 8/4 6/2(2), and double 1s).
I'm working on a revised (improved) puzzle of the same type, which I hope to post soon.
Nack