In order to make the excellent Half-Crossover concept (first written about by Douglas Zare in 2000 in this article, as far as I know) even faster, I developed the Kangaroo Count, first published in Flint Area Backgammon News (#277) in 2005.
It works to use Kangaroo Count for a comparative (relative) pipcount, but it occurred to me that I could supplement it with colorless counting when I read the terrific Urquhart/Simborg article (2012). It has long been known that the act of swapping two opposite-colored checkers on the board does not affect the relative pipcount, but it was Robert Urquhart who first parlayed this amusing fact (and still a revelation to some) into a pip counting system.
In Robert's system, step 1 accomplishes the same thing that the "far side men" (which could just as easily be near side men) and "big diagonals" do in Kangaroo's steps 1 and 2, while also cleverly adding a 15th-checker twist to render checker color irrelevant. And the counting of the so-called "near triads" is identical to the counting of the "small diagonals" (or "minor diagonals" or "diags") employed in Kangaroo -- other than how the math manifests. [By the way, there is a long standing definition of "near" that refers to the set of 12 points on the player's own side of the board, so Mr. Urquhart might want to consider changing his terminology of the small diagonals from "near triads" to "low triads."]
Finally, Urquhart's step 3 (to convert from an approximate count to an exact count) is essentially the same as the final step used in Kangaroo, which is the same as the final step in Zare's Half-Crossover system. I describe this step as "shifting to the Middles" (the second and fifth points of each quadrant) in order to clarify my process. I do not tally up a series of +1 and –1 adjustments for all eight triples / triads / half-quadrant. Typically all I need to actually "count" is a left-over pip or two, or no pips at all!
Some time back in the 1980s, I was at the Monte Carlo tournament, hanging out as usual the night before with (probably) KG, WGR and Senk. In one of these guy's hotel rooms was an open backgammon board and he asked my opinion about a checker play. I snickered (or maybe snackered): all thirty checkers were the same color. Or so I thought. It took me a couple of minutes to realize that the others weren't just playing along with the joke. They could see the position and I couldn't. This situation has never happened to that extent before or since, but I was handicapped by my partial color-blindness combined with the dim lighting and minimal color contrast of the checkers (something like maroon and brown). However, given what I know today, it occurs to me that I could have bewildered them with a comparative pipcount!
My new pipcount system, which is Kangaroo supplemented with colorless counting, is called "Coconut." This word incorporates the sounds at the beginning of each of the two words "Colorless Counting," which are also alliterative with the "K" in Kangaroo. Furthermore, the five letters of the word "count" appear in "coconut" almost in the same order. Finally, I (overactively) imagine coconuts might be a staple in the diet of kangaroos (which are mostly vegetarian), if they could only crack the shell. If you are nuts about the idea of colorless counting, try out Coco-nut!
The joy of Coconut (as with Kangaroo) is that you have to count only the number of checkers, not pips nor even crossovers. (And now, with the concept of colorless counting incorporated, you don't even have to distinguish Blue from White.) What a load off our minds.
Yes, for the Coconut system, as with Urquhart's, in which only the relative pipcount is to be ascertained, it makes no difference what color each of the thirty checkers are. It is useful to understand, however, that Blue and White each have their clearly designated sides of the board, bearoff trays and point numbers, which are often referenced. For example, there might be two checkers on White's 7pt, but for counting purposes we don't care one iota what color they are. They may as well be two different colors on the same point!
If you are not a mathematician, you might find it difficult to see exactly why Coconut (or the original Kangaroo Count) works, but it doesn't matter. Just follow the jingle below.
The poem for Coconut is:
.......First you double the near side men
.......Add big diagonal, double again
.......Add diags, minus 105, times 3
.......Then shift to the middles with glee
[That's if you want a "plus" number to mean that you are ahead. If you want a "plus" number to mean you are behind, then replace "near" in the first line with "far." In that case, the big diagonal will include the opponent's home board instead of your own, and the "diags" (small diagonals) will include (for example) the opponent's 1pt and 7pt, instead of your own.
The reason I have chosen to use the opposite of Kangaroo's direction for the big diagonal and diags is that it hardly matters otherwise, and I may as well make the presentation of Coconut here a bit more compatible with Urquhart's system (for those who want to try both).
In Kangaroo (i.e., for the absolute count), as published, the "big diagonal" includes the opponent's home board. By modifying the Kangaroo poem a little, I could have the big diagonal include our own home board instead.]
Here again are those steps from the Cocunut poem, spelled out longhand:
----------------------------------------------------------------------------------------------------------
(1) Count the number of checkers on the near side. Double that.
(2) Add the number of checkers on the "big diagonal." Double again.
(3) Add the number of checkers on the small diagonals, subtract 105, and multiply by 3.
(4) Shift to the middles (optional).
----------------------------------------------------------------------------------------------------------
I've chosen a position to count, more or less at random. I clicked on the first post of the recent DQ thread initiated by Leobueno, and it appeared that the pipcount could be a relevant (or even pivotal) factor both for the cube action and the proposed checker problem in his position.
       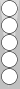                           |
| ||||
| XGID=---abBD-BB--cC---cBea-----:0:0:1:00:0:4:0:7:10 | |||||
Should Blue double in this position? Hmm, what is the race? | |||||
(1) Count the number of checkers on the near side. Double that.
Easy enough. 16 x 2 = 32.
(2) Add the number of checkers on the "big diagonal." Double again.
The "big diagonal" encompasses our home board (where there are 9 checkers) and the opponent's outer board (where there are 8 checkers). There are 17 checkers on the big diagonal.
So... 32 + 17 = 49, and double that to 98.
(3) Add the number of checkers on the low triads, subtract 105, and multiply by 3.
In the Kangaroo poem, "small diags," mean small diagonals. In the Coconut poem, the third line was syllabically cramped, so to better fit the meter, I've dropped the word small, and made "diag" (by itself) mean small diagonal. Anyway, there are two such "diags." One includes the lower three points (always from Blue's perspective) of the home boards (1-2-3, and 19-20-21). The other diag consists of the lower three points in the outer boards (7-8-9 and 13-14-15).
Find these four little areas (triples / triads / half-quadrants) on the diagram now and mentally imprint the diagonal flow of the two diags -- it will help you remember and boost your counting speed. Tom Keith has the shape of the diags (small/minor diagonals) well depicted here under "Step 3" there -- except for the moment be sure to ignore the location of the home boards there.
Here, there are 14 checkers on the diags. (See the checkers on Blue's 3pt plus White's 5pt and 6pt on the left, and on Blue's 8pt, 9pt and midpoint on the right -- add 'em up.)
Anyway... 98 + 14 = 112, subtract 105 becomes 7, times 3 makes 21.
Thus, Blue leads (we lead) by 21 pips. That is the approximate count.
Well... I see that this could be in the significant minority of positions where getting an approximate count may not be enough to ensure a proper cube decision and an exact count might be enough. Therefore, let's continue to step 4. But first, I'll repeat the diagram (so you don't have to scroll back and forth):
       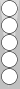                           |
| ||||
| XGID=---abBD-BB--cC---cBea-----:0:0:1:00:0:4:0:7:10 | |||||
(4) Shift to the middles. The "middles" are the middle points of the triples / triads / half-quadrants, which are perhaps most easily recognized as the second and fifth points of every quadrant. (Both players' 2pt, 5pt, 8pt and 11pt.) If a checker is located on a middle, its count is now zero and its job finished. What is left to do is to slightly adjust for the (typically) two-thirds of the checkers that are NOT already on their middles.
One way to account for the non-middle checkers is to add and subtract a series of 1-pip adjustments (as Urquhart implies in calling it a "Unit crossover count," and it works well enough, given that some pluses and minuses can be cancelled as you go). Relatively speaking, however, this process seems tedious to me. I prefer visual cancellation, which I find reduces the chance of error and minimizes actual "counting." Cancellation is speedy, not difficult, and actually fun -- you'll be surprised how good you can become with practice.
Our job is to get "rid" of the non-middle checkers in a series of transactions, either by making an (offsetting) shift that moves checker(s) to a middle, or finding some way to cancel them with other checkers or groups of checkers. Mental shifting involves a couple of basic concepts and several cancellation tricks, some of which I'll expound in more detail after you observe how I count the first position. For now, follow along as best you can.
There are many possible shifting approaches in this position, but here's the one that jumped out at me:
Move one of Blue's 5pt checkers back to his 6pt (note the vertical symmetry), and offset by sliding 3pt to 2pt. The entire left side of the board has vanished, except for the two checkers on Blue's 4pt, which is canceled against the (reflecting) 9pt. Yes, now completely vanished, because the checker shifted to the 2pt had already arrived at its middle -- poof! Likewise, the checkers on both 8pts vaporize (as always). And the midpoints vertically cancel, leaving only the surviving two checkers on White's 7pt, which are "high" and hence count –2 (high/negative being unfavorable for Blue's count).
Therefore, adjust the 21 (approximated earlier) by –2, for an exact difference of 19. That is, Blue leads by 19 pips.
[According to XGR++ evaluation: Blue should double at this match score (0–4 to 7), though it's a small non-double for money. At a score of 0–2 to 7, the doubling decision is borderline.
In his actual post, Leobueno put dice of 64 on the board. With this roll, breaking the 18pt anchor and coming around to the 8pt is easily best at all scores, in large part due to Blue's sizeable lead in the race. For example (according to ++), for money, the second best play is an error of .148. Conversely (though it is difficult to adjust pipcount without materially affecting distribution), if you move both of Blue's checkers from 9pt to 13pt, thereby reducing Blue's lead from 19 to 11 pips, hitting (13/3*) becomes the best play by a margin by .011, a swing of .159. That seems to confirm that the race does matter!]
I promised you some tips for shifting in Step 4. (Please forgive my laziness for not providing diagrams.) If it doesn't interest you at this time, skip to the next position.
For general shifting practice in pipcount systems, (1) checkers on the same (near vs. far) side of the board can be moved equally away from each other without altering the count. For example, you can move a checker 9/8 while moving another checker 1/2 (from 1pt to 2pt), a form of horizontal cancellation. And (b) checkers on opposite (near vs. far) sides of the board can be moved in the same (left/right) direction. For example, 10/11 can offset 21/20 or 18/17.
However, and this is important: In half-quadrant pipcount systems, the edge points of the triads are sacred: do NOT step over them (e.g., from 21pt to 22pt, or 7pt to 6pt); else your count will slip. For example, in this position, you might be tempted to move the 9pt checkers in opposite directions, so that you can get one of them to a middle (the 8pt), and the one going to the 10pt can be dealt with later. NO, not allowed. There is a triad barrier between the 9pt and 10pt, as real as the bar in the center of the board.
In the shifting process (my preferred way of converting approximation to exactitude in half-quadrant systems), vertical cancellation is not only allowed -- it is of enormous help. Notice that (in offsetting 3/2) I moved a checker OFF Blue's 5pt middle (back to the 6pt) to achieve a large vertical symmetry (alternatively, I could have achieved the same goal by moving White 6/5). In doing so, I made all the 6pt checkers go away (instead of removing four vs. four, which is less clean).
More vertical cancellation: Without shifting at all, the midpoints just disappeared like money-borrowers, never to be seen again. Granted, instead, I could have moved the three near-side midpoint checkers to the left, and the far-side midpointers likewise to the left (an equal offset), putting all six checkers on the 11pt and 14pt middles. But why go to the trouble? Vertical cancellation is instantaneous.
Even diagonal canceling works, for checkers on opposite sides of the board and exactly 3, or 6, or 9 pips to the left or right of each other. For example, I could have chosen to cancel the anchor on Blue's 4pt with the anchor on White's 7pt. Until recognition of this (or of any legitimate transaction) becomes automatic, you can (though less quickly) shift these anchors both to the right to find their middles.
[A wider (6-off) diagonal-offset example would be to cancel White's three midpointers with three of her 6pt checkers. I briefly considered it because then her remaining two 6pters could go to her 5pt middle, offset by Blue doing the same with his two 6pt spares, and demolishing the entire (symmetrical) eight-checker block on his 6-5-4. My instincts may have rebelled leaving the other midpoint isolated in the process, though when you gain enough speed and confidence, typically whatever you see first is best.]
With practice, entire boards can sometimes empty themselves in a second or two.
----------------------------------------------------------------------------------------------------------
Finally, let's use Coconut to count Position 1 of the Urquhart/Simborg article. Beforehand (or afterwards), for comparison, you might want to read their version of the count by clicking here and then on DOC.
Okay, here's how the same position can be counted using Coconut:
                                  |
| ||||
| XGID=----CbC-C---bB--bcCbb-b-A-:0:0:1:00:0:0:3:0:10 | |||||
(1) Count the number of checkers on the near side. Double that.
Simple. 13 x 2 = 26.
(2) Add the number of checkers on the "big diagonal." Double again.
On the big diagonal, there are 8 + 10 = 18 checkers. So... 26 + 18 = 44, and double that to 88.
(3) Add the number of checkers on the small diagonals, subtract 105, and multiply by 3.
There are only 9 checkers on the low triads, comprising the small diagonals. (See White's 6pt and 5pt, and Blue's 8pt and midpoint.) Anyway... 88 + 9 = 97, subtract 105 becomes –8, times 3 makes our count –24 .
Thus, Blue trails (we trail) by 24 pips, approximately. If you want an exact count, finish off with...
(4) Shift to the middles.
The midpoints cancel. Blue's entire 6-5-4 group is symmetrical around its middle (his 5pt), already done. Likewise with the 7pt-9pt group on White's side, except for the spare on her 7pt, which symmetrically cancels against one of her 6pt checkers, and the other 6pt checker horizontally cancels against her 1pt blot! And of course White's 5pt and Blue's 8pt are ignored (already at their middles).
Only two checkers survive: on White's 3pt. They are (both) 1 pip on the low side of their respective triads, so the count is +2 (i.e., in favor of Blue). Adding the +2 to the –24 gives you the exact count. Blue is behind by 22 pips.
Running the steps together:
13 x 2 = 26... +18 = 44, x 2 = 88... +9 = 97, -105 = –8, x 3 = –24..... +2 = –22.
The blue numbers represent the three times you actually counted checkers (and the one time in green when you counted all of 2 pips). The rest of the numbers represent (what will become for you) routine arithmetic.
Nack