Casper wrote: You can work this out by making a realistic assumption about the cubeless win percentages, and then give white the cube vig. For example, if you say for simplicity that Blue is 60-40 cubeless, no gammons, and that cube vig adds 1/5th of white wins, White ends up losing 0.04 on the 2 cube. These numbers were a bit shaded towards White, so it is even worse than that.
I thought that was interesting and reasonable. Casper suggests that if Blue's gammon-adjusted GWC is 60%, then Blue's cubeless equity = 0.600 - 0.400 = +0.200. And if holding the cube multiplies White's gammon-adjusted wins by 1.2, then White wins the equivalent of 0.400 * 1.2 = 48%, and Blue's equity with White holding a 2-cube = 0.520 - 0.480 = +0.040.
Similarly, if Blue wins 79.16% cubeless, then Blue's cubeless equity = 0.7916 - 0.2083 = +0.5833 (a big pass since 2 * 0.5833 = 1.166). But if holding the cube multiplies White's gammon-adjusted wins by 1.2, then White wins 0.2083 * 1.2 = 0.250, and Blue's equity = 0.750 - 0.250 = +0.500 (giving White a borderline drop/take since 0.500 * 2 = 1).
I chose 79.16 to conveniently fit both Casper's suggestion that cube equity be assumed to add 1/5 to the underdog's wins and to illustrate the familiar concept that we can take a cube with less than 25% cubeless GWC because holding the cube is worth something (although rarely will it be worth as much as 4.17% extra GWC).
Another approach (similar to Casper's) to the original proposition would be: in the continuous model of a cubeful game, you can take with 20% cubeless GWC, but if you can never redouble, you need 25%. So the cube is worth 5% GWC in the continuous model. If holding the cube against an opening 1-1 reduces the opener's gammon-adjusted GWC by 5%, then the opener has the better side of the proposition as long as his gammon-adjusted cubeless GWC is more than 55%. And clearly he must have at least that much. For comparison, an opening 3-1 rolls out to be worth 0.167 cubeless equity, which is the gammonless equivalent of winning 58.35% (the real cubeless GWC isn't that high because some of that equity is from net gammon wins). If holding the cube reduces the opener's cubeless gammon-equivalent wins from 58.35% to 53.35%, the 3-1 side is still clearly better off than the side holding the cube.
Back to Casper's suggestion, where +0.040 equity is worse than +0.200, but still more than 0.000. I thought, wait a moment, that +0.040 should be doubled to +0.080, since the cube is on two. But then I thought: the +0.200 should also be increased, since that's cubeless with a centered cube; the opener's equity has to be higher than +0.200, as a 60/40 favorite with cube access. But how much higher? Which brought me to this reference position:
Unlimited match, Blue on roll.
| White | 70 | ||
|---|---|---|---|
                    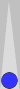              | |||
| Blue | 70 | ||
| Position ID: 2r0PAADavQ8AAA Match ID: cAkAAFAAGAAE | |||
1) Blue's cubeless GWC is very close to 60%.
2) That's why Blue's cubeless equity = 0.600 - 0.400 = ~0.200 (or 0.201, as you see).
3) The position is not good enough to double, so the cube should stay centered for at least one turn. But since Blue has cube access, his cubeful equity with a centered cube is not +0.200, but +0.304, which is the equivalent of winning about 65% cubeless, instead of 60%. So cube access is worth about the equivalent of 5% GWC to Blue.
4) So, cubeless, the position is worth +0.200 with a centered cube, equivalent to 60% GWC. With correct cube action, Blue's cubeful equity is +0.304, equivalent to about 65% cubeless GWC. If Blue incorrectly doubles, Blue's cubeful equity is only +0.140, equivalent to winning 57% cubeless. So what's cube ownership worth to White? The equivalent of 8% GWC, compared to Blue's equity with a centered live cube; the equivalent of 3% GWC, compared to Blue's cubeless equity.
Alert: wrong double ( -0.164)! [very bad]
| Cube decision | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rollout cubeless equity | +0.201 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cubeful equities: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. | No double | +0.304 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | Double, pass | +1.000 | +0.696 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | Double, take | +0.140 | -0.164 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Proper cube action: | No double, take (19.1%) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rollout details | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Full cubeful rollout with var.redn. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1296 games, Mersenne Twister dice gen. with seed 689099689 and quasi-random dice | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Play: world class 2-ply cubeful prune [world class] | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| keep the first 0 0-ply moves and up to 8 more moves within equity 0.16 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Skip pruning for 1-ply moves. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cube: 2-ply cubeful prune [world class] | |||||||||||||||||||||||||||||||||||||||||||||||||||||
Another position:
| White | 70 | ||
|---|---|---|---|
                   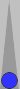 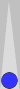              | |||
| Blue | 61 | ||
| Position ID: 2r0PAAC1vQcAAA Match ID: cAkAAAAAAAAE | |||
Blue's cubeless equity is +0.596, Blue wins about 80% cubeless (79.8%), and 0.798 - 0.202 = 0.596. The position is a pass. But holding the cube has some value for White. If it had no value, Blue's cubeful equity would 0.596 * 2 = 1.189 (times 2 because the cube goes to 2). But Blue's cubeful equity is only +1.076. If we divide +1.076 by 2 (to get rid of the effect of doubling the cube value), we get +0.538, and
0.769 - 0.231 = 0.538
In other words, holding the cube is worth the equivalent of 0.798 - 0.769 = 2.9% GWC to White.