When the Safe Harbor Games dice problem first came up in 2009, I didn't like the solution, but didn't give it too much thought, except to think I'd never want to play there. Now I think ... ludicrous might be the right word? Whether the game in the "red room" should be called "backgammon" I don't know. But for any of those casual players who are at all interested in learning more about how to play the game, the "red room" isn't the place to apply even very basic knowledge. And worse, the many ways in which "red room" dice are misleading those players aren't even obvious. I don't think that's "good for the game."
Henrik wrote:A lot of stuff will change,
Indeed. I first thought -- well, good luck applying standard race formulas to a game where doubles are only half as frequent! But it's not just races. Take a look at this standard double/take reference position:
Unlimited match. Blue on roll
| White | 2 | ||
|---|---|---|---|
                    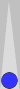   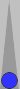           | |||
| Blue | 7 | ||
| Position ID: AwAAEAEAAAAAAA Match ID: cAkAAAAAAAAE | |||
Is it not true that if doublets occur only half as often as expected, this isn't even a double? If my calculations are wrong, please tell me how:
There are 6/36 doublets and 30/36 nondoublets. With normal dice, doublets occur 16.66% of the time, so nondoublets must occur 83.33% of the time. But if you halve the chance of rolling any doublet, then that chance is only 8.33%. And the chance of rolling any nondoublet must be 91.67%. Which means that the chance of rolling a specific doublet with "Red Room" dice is only 1.38%, and the chance of rolling a specific nondoublet has to be 6.11%.
| Normal Dice | "Red Room" dice | |
| Chance of rolling any doublet: | 16.66% | 08.33% |
| Chance of rolling any nondoublet: | 83.33% | 91.67% |
| Chance of rolling specific doublet: | 02.77% | 01.38% |
| Chance of rolling specific nondoublet: | 05.55% | 06.11% |
In the position above, there are 19 rolls that bear off, a 52.77% chance. These good rolls are the 5 good doublets and 2 * 7 = 14 nondoublets. With normal dice:
| 5 | * | 2.7777 | = | 13.8888 |
| 7 | * | 5.5555 | = | 38.8888 |
| 52.7777 |
With "red room" dice:
| 5 | * | 1.3888 | = | 06.9444 |
| 7 | * | 6.1111 | = | 42.7777 |
| 49.7222 |
Perhaps reducing doubles "by half" was only an approximation. Perhaps the frequency of doublets in the Red Room is 9.22%, not 8.33%. In that case,
| Normal Dice | "Red Room" dice | |
| Chance of rolling any doublet: | 16.66% | 09.22% |
| Chance of rolling any nondoublet: | 83.33% | 90.77% |
| Chance of rolling specific doublet: | 02.77% | 01.53% |
| Chance of rolling specific nondoublet: | 05.55% | 06.05% |
and
| 5 | * | 1.5366 | = | 07.6833 |
| 7 | * | 6.0518 | = | 42.3626 |
| 50.0459 |
and the position is a double, but just barely.
Examples of how skewing the percentage of doublets change many aspects of the game can be multiplied. For example, how often does Blue hit here?
Unlimited match. Blue on roll
| White | 7 | ||
|---|---|---|---|
  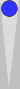                                | |||
| Blue | 26 | ||
| Position ID: QAAADAAACAAAAA Match ID: UQkAAAAAAAAE | |||
47.22% of the time? Or, if you don't know that percentage, 17/36? Not with "red room" dice:
| with 8.33% doublets | with 9.22% doublets | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | * | 1.3888 | = | 04.1666 | 3 | * | 1.5366 | = | 04.6098 |
| 7 | * | 6.1111 | = | 42.7777 | 7 | * | 6.0518 | = | 42.3626 |
| 46.9444 | 46.9724 | ||||||||
Another standard reference position:
Unlimited match. Blue on roll.
| White | 6 | ||
|---|---|---|---|
                        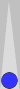          | |||
| Blue | 6 | ||
| Position ID: IAAAgAAAAAAAAA Match ID: UQkAAAAAAAAE | |||
Every backgammon student who plays with normal dice learns that this position is a double and an optional take. With normal dice in 100 games, White loses 200 points passing, and 200 points taking. I could note, also, that the position lends itself to teaching, since 3/4 or 27/36 of Blue's rolls bear off, and 1/4 don't, leading to a redouble after which, if Blue takes, Blue wins 1/4 of that 1/4. Blue wins 3/4 * 4 + ((1/4 * (3/4 - 1/4) * 8) points, etc. Easy numbers for practicing backgammon related calculations.
With red room dice (of either flavor), neither player bears off 75% of the time on roll, and the position is simply a take. Passing gives up about 0.03 points per game.
Here's another standard reference position:
Unlimited Match. Blue on roll.
| White | 8 | ||
|---|---|---|---|
                                  | |||
| Blue | 8 | ||
| Position ID: /wAAAP4BAAAAAA Match ID: cAkAAAAAAAAE | |||
With normal dice, Blue on roll wins 74.5% cubeless and the position is a double/take. Dropping is an 0.083 blunder. But what's the right cube action with red room dice, where doublets occur either 8.33% or 9.22% of the time? Care to guess, or calculate, how big of a mistake the wrong cube action is?