BGonline.org Forums

Early game sequence, 54D-61P-65P-54D-652-65P-32, etc.

Posted By: Nack Ballard
Date: Sunday, 3 December 2017, at 6:57 a.m.

In Response To: Standard Checker Play - Rollout and VARIANT (Nack Ballard)

Stick's fine position with the triple-blotting 32 play, along with my cusp variant, is shown here.

I got curious about switching the order of White's roll of 62 and Blue's roll of 32.

For the first part of that equation, suppose White has not played her 62D yet, as shown below, and Blue has 32 to play. Now what?
Cover up the rollout details below the diagram until you are ready to compare your answer.

		White is Player 2 score: 0 pip: 140 Unlimited Game Jacoby Beaver pip: 136 score: 0 Blue is Player 1
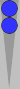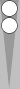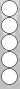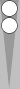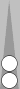XGID=-bAB--E-C---bB---bbe--b-B-:0:0:1:32:0:0:3:0:10
54D-61P-65P-54D-652-65P-32

1.	Rollout1	8/3	eq: -0.554
	Player: Opponent: 36.50% (G:10.61% B:0.59%) 63.50% (G:21.35% B:1.48%) Conf.: ± 0.007 (-0.560...-0.547) - [99.1%] Duration: 10 minutes 55 seconds
2.	Rollout1	8/5 6/4	eq: -0.565 (-0.011)
	Player: Opponent: 37.68% (G:11.33% B:0.55%) 62.32% (G:24.66% B:3.00%) Conf.: ± 0.007 (-0.572...-0.558) - [0.9%] Duration: 11 minutes 14 seconds
3.	Rollout1	24/21 8/6	eq: -0.585 (-0.032)
	Player: Opponent: 37.02% (G:11.88% B:0.92%) 62.98% (G:28.42% B:1.65%) Conf.: ± 0.010 (-0.595...-0.575) - [0.0%] Duration: 11 minutes 33 seconds
4.	Rollout1	6/4 6/3	eq: -0.587 (-0.033)
	Player: Opponent: 36.41% (G:10.51% B:0.53%) 63.59% (G:22.62% B:2.14%) Conf.: ± 0.008 (-0.594...-0.579) - [0.0%] Duration: 11 minutes 23 seconds
5.	Rollout2	13/8	eq: -0.607 (-0.054)
	Player: Opponent: 34.76% (G:9.90% B:0.58%) 65.24% (G:20.24% B:1.60%) Conf.: ± 0.009 (-0.616...-0.598) - [0.0%] Duration: 5 minutes 51 seconds
6.	Rollout2	13/11 13/10	eq: -0.608 (-0.054)
	Player: Opponent: 35.23% (G:10.27% B:0.54%) 64.77% (G:20.84% B:1.87%) Conf.: ± 0.010 (-0.617...-0.598) - [0.0%] Duration: 6 minutes 07 seconds
7.	Rollout2	13/11 6/3	eq: -0.612 (-0.059)
	Player: Opponent: 34.83% (G:10.49% B:0.59%) 65.17% (G:22.02% B:2.14%) Conf.: ± 0.013 (-0.626...-0.599) - [0.0%] Duration: 5 minutes 37 seconds
8.	Rollout3	13/11 8/5	eq: -0.652 (-0.098)
	Player: Opponent: 35.77% (G:10.65% B:0.63%) 64.23% (G:25.42% B:3.73%) Conf.: ± 0.024 (-0.676...-0.628) - [0.0%] Duration: 3 minutes 17 seconds
1 5184 Games rolled with Variance Reduction. Dice Seed: 16319810 Moves: 3-ply, cube decisions: XG Roller 2 2592 Games rolled with Variance Reduction. Dice Seed: 16319810 Moves: 3-ply, cube decisions: XG Roller 3 1296 Games rolled with Variance Reduction. Dice Seed: 16319810 Moves: 3-ply, cube decisions: XG Roller

So, 8/3 goes from being worse than 8/5 6/4 by .076 (in Stick's original position) to being better than 8/5 6/4 by .011 (above).

Can't stomach 8/3? Okay, say Blue plays 8/5 6/4 anyway (leaving three inside blots). With White on roll, what is the correct cube action?
Cover up the rollout details below the next diagram until you are ready to compare your answer.

		White is Player 2 score: 0 pip: 140 Unlimited Game Jacoby Beaver pip: 131 score: 0 Blue is Player 1
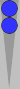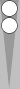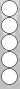XGID=-bABAAD-B---bB---bbe--b-B-:0:0:-1:00:0:0:3:0:10
54D-61P-65P-54D-652-65P-32&-C

Analyzed in Rollout	No double	Double/Take
Player Winning Chances:	62.41% (G:25.13% B:3.08%)	62.20% (G:25.60% B:3.41%)
Opponent Winning Chances:	37.59% (G:11.32% B:0.55%)	37.80% (G:11.44% B:0.56%)
Cubeless Equities	+0.412	+0.828
Cubeful Equities
No double:	+0.568	±0.008 (+0.561..+0.576)
Double/Take:	+0.540 (-0.028)	±0.011 (+0.529..+0.551)
Double/Pass:	+1.000 (+0.432)
Best Cube action: No double / Take
Percentage of wrong pass needed to make the double decision right: 5.8%
Rollout details
5184 Games rolled with Variance Reduction. Dice Seed: 16319810 Moves: 3-ply, cube decisions: XG Roller
Double Decision confidence:		100.0%
Take Decision confidence:		100.0%
Duration: 30 minutes 15 seconds

So, now we have Ken's rollout of Stick's original position (for which White has already played 62D), where White's cube turn is right by about .03, contrasted to this position (no White 62D yet), where White's cube turn is wrong by about .03.

Okay, White dutifully decides NOT to double. How should she play 62 above?
Compare your answer to the one supported by the rollout below.

		White is Player 2 score: 0 pip: 140 Unlimited Game Jacoby Beaver pip: 131 score: 0 Blue is Player 1
XGID=-bABAAD-B---bB---bbe--b-B-:0:0:-1:62:0:0:3:0:10
54D-61P-65P-54D-652-65P-32&-62

1.	Rollout1	13/7 6/4	eq: +0.031
	Player: Opponent: 51.43% (G:18.26% B:1.73%) 48.57% (G:19.06% B:1.68%) Conf.: ± 0.008 (+0.023...+0.038) - [100.0%] Duration: 8 minutes 10 seconds
2.	Rollout1	24/16	eq: -0.002 (-0.032)
	Player: Opponent: 51.56% (G:15.60% B:1.45%) 48.44% (G:21.67% B:0.65%) Conf.: ± 0.008 (-0.009...+0.006) - [0.0%] Duration: 10 minutes 24 seconds
3.	Rollout1	13/11 13/7	eq: -0.010 (-0.041)
	Player: Opponent: 49.85% (G:16.64% B:1.52%) 50.15% (G:17.29% B:1.07%) Conf.: ± 0.008 (-0.018...-0.002) - [0.0%] Duration: 8 minutes 32 seconds
4.	Rollout2	24/18 6/4	eq: -0.054 (-0.085)
	Player: Opponent: 50.80% (G:17.82% B:1.83%) 49.20% (G:26.11% B:1.35%) Conf.: ± 0.013 (-0.067...-0.041) - [0.0%] Duration: 2 minutes 32 seconds
5.	Rollout2	13/5	eq: -0.056 (-0.087)
	Player: Opponent: 49.22% (G:17.50% B:1.76%) 50.78% (G:20.16% B:1.95%) Conf.: ± 0.015 (-0.071...-0.041) - [0.0%] Duration: 2 minutes 11 seconds
1 5184 Games rolled with Variance Reduction. Dice Seed: 34514706 Moves: 3-ply, cube decisions: XG Roller 2 1296 Games rolled with Variance Reduction. Dice Seed: 34514706 Moves: 3-ply, cube decisions: XG Roller

In short, assuming we can trust the rollouts, swapping the order of rolls altered both Blue's best play (with 32) and White's (with 62).

Let's go a step further: After White double-blots with $ (Slot, 13/7 6/4), how should Blue play 63?
Cover up the rollout details below the next diagram until you are ready to compare your answer.

		White is Player 2 score: 0 pip: 132 Unlimited Game Jacoby Beaver pip: 131 score: 0 Blue is Player 1
XGID=-bABAAD-B---aB---bcd-ab-B-:0:0:1:63:0:0:3:0:10
54D-61P-65P-54D-652-65P-32&-62$-63

1.	Rollout1	8/5 8/2	eq: +0.025
	Player: Opponent: 49.08% (G:18.98% B:1.41%) 50.92% (G:16.05% B:1.18%) Conf.: ± 0.008 (+0.017...+0.033) - [68.8%] Duration: 7 minutes 25 seconds
2.	Rollout1	24/21* 8/2	eq: +0.022 (-0.003)
	Player: Opponent: 49.86% (G:22.10% B:2.73%) 50.14% (G:22.31% B:2.77%) Conf.: ± 0.008 (+0.015...+0.030) - [31.2%] Duration: 7 minutes 49 seconds
1 5184 Games rolled with Variance Reduction. Dice Seed: 34514706 Moves: 3-ply, cube decisions: XG Roller

TCTC.

One final tease: Say Blue quietly covers two inside points (8/5 8/2) with 63. How then should White play 31?
Cover up the rollout details below the next (final) diagram until you are ready to compare your answer.

		White is Player 2 score: 0 pip: 132 Unlimited Game Jacoby Beaver pip: 122 score: 0 Blue is Player 1
XGID=-bBBABD-----aB---bcd-ab-B-:0:0:-1:31:0:0:3:0:10
54D-61P-65P-54D-652-65P-32&-62$-63J-31

1.	Rollout1	8/5 6/5	eq: -0.039
	Player: Opponent: 50.57% (G:15.33% B:1.14%) 49.43% (G:25.96% B:4.40%) Conf.: ± 0.005 (-0.044...-0.033) - [100.0%] Duration: 4 minutes 33 seconds
2.	Rollout1	7/4 6/5	eq: -0.058 (-0.019)
	Player: Opponent: 50.34% (G:14.86% B:1.14%) 49.66% (G:22.96% B:2.78%) Conf.: ± 0.007 (-0.064...-0.051) - [0.0%] Duration: 6 minutes 26 seconds
3.	Rollout2	8/4	eq: -0.145 (-0.106)
	Player: Opponent: 46.57% (G:15.07% B:1.14%) 53.43% (G:21.83% B:2.34%) Conf.: ± 0.013 (-0.158...-0.132) - [0.0%] Duration: 1 minute 13 seconds
4.	Rollout2	24/21* 4/3	eq: -0.175 (-0.136)
	Player: Opponent: 45.87% (G:14.35% B:1.21%) 54.13% (G:22.00% B:1.33%) Conf.: ± 0.014 (-0.189...-0.160) - [0.0%] Duration: 2 minutes 03 seconds
1 5184 Games rolled with Variance Reduction. Dice Seed: 34514706 Moves: 3-ply, cube decisions: XG Roller 2 1296 Games rolled with Variance Reduction. Dice Seed: 34514706 Moves: 3-ply, cube decisions: XG Roller

The results of the last two rollouts should remind us that when in doubt, make the 5pt (unless you move your threshold of doubt too far the other way).

Nack

Messages In This Thread

• Standard Checker Play
  Stick -- Wednesday, 29 November 2017, at 10:19 a.m.
  • Standard Checker Play
    John O'Hagan -- Wednesday, 29 November 2017, at 3:23 p.m.
    • Standard Checker Play
      Stick -- Wednesday, 29 November 2017, at 7:25 p.m.
      • Standard Checker Play
        neilkaz -- Wednesday, 29 November 2017, at 7:28 p.m.
      • Standard Checker Play
        John O'Hagan -- Wednesday, 29 November 2017, at 8:17 p.m.
  • Standard Checker Play
    Karol Szczerek -- Wednesday, 29 November 2017, at 4:42 p.m.
  • Standard Checker Play
    ah_clem -- Wednesday, 29 November 2017, at 9:46 p.m.
  • Same position in a match
    KenB -- Thursday, 30 November 2017, at 7:59 p.m.
    • Same position in a match
      ah_clem -- Thursday, 30 November 2017, at 9:04 p.m.
    • Same position in a match - rollout
      KenB -- Friday, 1 December 2017, at 3:54 p.m.
    • After the triple slot - cube
      KenB -- Friday, 1 December 2017, at 4:09 p.m.
  • Standard Checker Play - Rollout
    Stick -- Friday, 1 December 2017, at 9:03 a.m.
    • Standard Checker Play - Rollout and VARIANT
      Nack Ballard -- Saturday, 2 December 2017, at 3:05 a.m.
      • Early game sequence, 54D-61P-65P-54D-652-65P-32, etc.
        Nack Ballard -- Sunday, 3 December 2017, at 6:57 a.m.
        • 54D-61P-65P-54D-652-65P-32 -- 4-ply rollout
          Nack Ballard -- Sunday, 3 December 2017, at 3:55 p.m.