Max has explained his Criss-Cross system, but I thought it might help to chime in with my own explanation as well (another perspective, if you will).
To my knowledge, Douglas Zare created the first pipcount system based on three-point groups, which he called "half-crossover." This has since become a generic term defining any system that uses three-point groups -- in the same way that the brand names "kleenex" (for tissue) or "xerox" (for photocopy) caught on.
If you imagine a vertical dividing line running down the middle of each quadrant, between the 3pt and 4pt, and between the 15pt and 16pt, of both players, you can see that the board is divided into eight of these half-crossovers (three-point groups). Zare, myself and other people who have written about various half-crossover systems have referred to these point-groups as "triples," "triads," "zones" or "half-quadrants."
I'm now introducing "SLICE" as yet another synonym for a half-quadrant: think of each one as a quadrant sliced in half. (It will later become clear why I've selected this term.)
                                  |
| ||||
| XGID=--------------------------:0:0:1:00:0:0:0:11:10 | |||||
Instead of numbering points 1 to 24, Zare numbered slices (my term for three-point groups) essentially "1" to "8" and multiplied by 3. Then, though, he wisely subtracted 2 from each slice, numbering them instead "–1" through "+6" as shown in the above diagram. [A single adjustment of +90 at the end (the just-mentioned 2, times 3 points-per-slice, times 15 checkers) translates to the traditional pipcount.] In this way, numbers (upon which calculations are performed) are smaller and it becomes possible to benefit from +/– cancellation. (You might recognize this advantageous technique from Naccel, where the inner board is –1 and the outer board is +1.)
It is common knowledge that any traditional point number added to its vertically corresponding point number sums to 25 (e.g., Blue's 21pt is White's 4pt, and 21 + 4 = 25). In a similar manner, any slice number (see diagram) added to its vertically corresponding slice number sums to 5 (e.g., the 1-slice and 4-slice are opposite each other, and 1 + 4 = 5).
Max harnessed this 5-sum in order to work with even smaller numbers and more cancellations/offsets. I will now repeat the slice-numbering above on the diagram below, except I'm subtracting 5 from the upper numbers. Further, I'm replacing the two zeros with blanks, the "+2" with "++" (same meaning), and the "–2" with "– –" (same meaning).
                   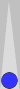   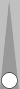         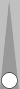   |
| ||||
| XGID=-A--aBCBB-Caa-aa-bcc-bA-A-:0:0:1:00:0:0:3:0:10 | |||||
If you go to Max's page and scroll down a bit, you will see that his plusses and minuses are laid out the same way; I've merely reproduced and explained them. (Sorry about the horizontal reversal. I don't know how to create a diagram at bgonline with the inner boards on the right; mine are on the left.)
If you like, you can work your way around the board, adding and subtracting (or double-adding and double-subtracting, near the midpoints) the number of checkers in each slice. Not bad, but soon I'll show you a faster way.
To bring the count back in line with Zare's numbering (–1 to +6) marked on the previous diagram, you can count to see how many more checkers exist at the top than 15 (which is half the total number of checkers, a constant). In this case, there are 14 at the top, which makes the excess –1. This excess needs to be multiplied by 5 (review the paragraph preceding the above diagram) and added back in.
Is there a faster way than counting all 14 checkers on top? Yes! Instead, just count the number of Blue checkers on top and subtract the number of White checkers on the bottom. For this position, that's 2 – 3 = –1. Elegant. (This is the one time that distinguishing checker color is profitable in a colorless system.)
Those steps bring you to an approximate count, sufficiently close that the final step will usually be unnecessary. In the event it is needed, you adjust (as in all half-crossover systems) for checkers that are 1 pip away (or 2 away in the case of checkers on the roof or borne off) the center of their slices. I discuss various shortcuts here (scroll down to "(4) Shift to the Middles," from there to the dotted line).
Going back to Zare's scheme, to restore the traditional pipcount it is necessary to multiply by 3, add 90 and 1-pip shift within slices (if needed). Is it worth it? Well, clearly Zare believed in the net gain enough to publish his half-crossover system. And as my summary has shown, the only two modifications added by Criss-cross are (1) the count of the far-side slices is reduced by 5, and (2) it is colorless -- the modern gain of speed in exchange for determining only relative count (not totals).
In part, the value of any system is a matter of personal taste, but it seems to me that most people rush to judgment without practicing at least a dozen full-position counts.
I created a little jingle to help remember the steps to the Criss-cross system. For best results, recite it aloud a couple/few times. To make the meter go smoothly, put stress on the syllables in boldface.
.....Criss minus Cross; add Mid diff'rence twice.
.....Plus far-minus-near times five; all thrice.
.....To hone, you cancel or shift in each slice.
Now it is clear why I created the (half-quadrant) synonym "slice." It rhymes.
These lines represent, respectively, what Max refers to as "step 1," "step 2" and "step 3." While admittedly arbitrary, it is more convenient for me to view these as five steps, using the semi-colons in the first two lines as dividers. However, I will number these "five" steps 1a, 1b, 2a, 2b, and 3, so that you can read both Max's walk-through of the count (if you like), and my own, without confusion.
I am not skilled enough with html to circle groups. Instead, where relevant, I will isolate the key checkers in separate diagrams.
                   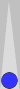               |
| ||||
| XGID=-A-----BB--------bc---A-A-:0:0:1:00:0:0:3:0:10 | |||||
Remember: the color of the checkers makes no difference.
Step 1a (Criss minus Cross): Above, the six checkers in the two plus (+) slices is the same as the number of checkers in the minus (–) slices. Therefore, our count so far is zero. Quoting the famous line in Alfred Hitchcock's Strangers on a Train (forward to the 1:30 and 2:10 marks on the video): "Criss-cross!"...Next...
                               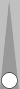   |
| ||||
| XGID=----------Caa-aa----------:0:0:1:00:0:0:3:0:10 | |||||
Step 1b (add Mid difference twice): Checkers in the midpoint slice count double (+2 or –2). Here, 10 minus 4 equals 6 (or if you prefer, 5 minus 2, times 2 = 6). Add it to the criss-crossed count (we did in step 1a), which was zero, gives us a count of 6 (so far).
Below, I've removed (the props of) the plus and minus signs and included all checkers. Can you still see steps 1a and 1b? Ignore the checkers on both players' 4-5-6pt slices (they count zero). Flanking that swatch, train your eyes to see the "criss-cross," which in this case is 6 vs 6 (these checkers all neatly cancel). All that remains is the midpoint swatch on the far right, ++ at the bottom and – – at the top (i.e., 10 minus 4).
                   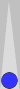   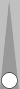         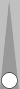   |
| ||||
| XGID=-A--aBCBB-Caa-aa-bcc-bA-A-:0:0:1:00:0:0:3:0:10 | |||||
Step 2a (Plus far-minus-near times 5): All checkers are inspected for opposite-color status. Two blue far-side checkers minus three White near-side checkers equals –1. Multiply that by 5, equals –5.
The accumulative account was 6. Now it has become 1.
Step 2b (all thrice): Triple the whole thing. Our accumulative count grows from 1 to 3.
You now have a good approximate count. Blue's pipcount is 3 higher than White's; in other words, Blue trails by 3.
Step 3 (To hone, you cancel or shift in each slice): Max created a good diagram for this (scroll down to "Step 3"). This is the only non-trivial stage of the count but it can often be skipped.
It might be easier to follow Max's explanation because he has superior graphics, but I'll offer an alternate way to count it. Here is a re-diagram:
                                  |
| ||||
| XGID=-A--aBCBB-Caa-aa-bcc-bA-A-:0:0:1:00:0:0:3:0:10 | |||||
Cancel or shift to center point in each slice | |||||
(Checker color is irrelevant, but point-numbering will be described from Blue's point of view.)
- The slice with two Blue back checkers is already symmetrical around its center point.
- 15/14 and 19/20 take care of their respective slices. These 1-pip adjustments offset.
- The remaining far-side slice (outer board) needs 18/17(3); to offset that do 10/11(3).
- The "stranded" but planned 12pt blot is symmetrical with the 1pt blot. Still no change.
- All that remains is 7/8(2) and 6/5(2); these offset. Final assessment: No change in count.
Thus, there is no change to the +3 count that was accumulated in the previous steps.
In short, the full count (accumulatively) went:…..0...6...1...3...3
Nack