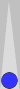I don't think anyone responded to you with ridicule, and I don't think you have any basis for calling anyone a "hypocrite" for not responding to all of your arguments or for failing to keep responding to you when you ignore what they say or repeat your arguments.
In fact, you got serious responses to several of your arguments. These responses explained why the responders disagreed with you. From those responses, you should have seen why some of your other statements were also thought to be wrong. How many more responses should you expect?
You write:
I said that if you make an error of 10% MWC your winning percentage becomes 45% and if you make an error of 60% it becomes 20%. They said that in the first case it becomes 40% but not being correct they said nothing for the second case.
Actually, you were shown a position that demonstrated how and why an error in that position that a bot evaluation says costs you 10% MWC error reduces your chance of winning the match by exactly 10%, according to the evaluation. Not by 5%. In that position, where the wrong cube decision costs 10% MWC, your chance of winning the match is 50% if you do not make a mistake (you correctly pass) but only 40% if you do make a mistake (you incorrectly take).
As far as I can see, you ignored this demonstrative example in your further comments in this discussion.
From that one example, you should have figured out for yourself that if the responders think of a 10% MWC error as reducing the probability of winning a match by 10%, not by 5%, then they also think of a 20% MWC error as reducing the probability of winning a match by 20%, and a 60% MWC error as reducing the probability of winning a match by 60% -- not 10% and 30%, or some other number arrived at by a formula which irrelevantly considers whether that total 20% or 60% MWC error occurred in one mistake or two, six or sixty separate errors.
From that one example, you should also have seen that the responders think MWC error is additive, not multiplicative, because whether or not previous errors were made in the play leading to that example position makes absolutely no difference in the calculation of the size of the error made in the example position. There, the error costs 10% MWC, and your expected winning percentage is reduced absolutely by 10%. It makes no difference how many errors were made by whom in what order previously. And it makes no difference what your MWC would be with correct play. If the right play attains 37% MWC, and the wrong play 27%, it's a 10% error.
MWC, after all, stands for "match winning chances." As far as I can see, that's the equivalent of "winning percentage," especially when you yourself sometimes use the terms to mean the same thing (as, for example, when you write "Because of some previous errors your winning percentage is now 40%. You make one error of 20% MWC." I don't know what "winning percentage" can mean there except "MWC.")
I think the problem you actually mean to address is something quite different. I think what you actually mean is that a bot's measurement of differences in relative skill -- i.e., differences in error rate derived from MWC error -- is an inaccurate predictor of win rate, as measured by the bot's translation of error rate to elo rating. Apparently, you believe that giving MWC errors different weight depending on when and where they occur in a match makes for a better predictor. I don't think you've demonstrated that. It's certainly not immediately obvious to me that if I make an error after my opponent makes an error, or if I make an error when my MWC is less than 50%, it should count less than if I make an error first, or make an error when my MWC is greater than 50%.
You write:
For years some players noticed that they win against the bot much more that they should as reported by the bot. Their observations were ridiculized on various bg forums.
I have no idea how accurately Snowie relative ER maps to relative elo. You might provide links, but I'm not sure it matters anymore, since XG plays better and costs less. With regard to Gnubg, my understanding is that several versions ago, it was realized that the "luck based FIBS rating difference" and the "error based absolute FIBS rating" were or had become broken, however well or badly they worked before.
An example of this is two one-point matches I analyzed today.
The first two rolls were the same in each match, and Player White and Player Blue made the same misplay on these two rolls. They played perfectly thereafter (according to 0-ply analysis). The first roll was 3-1, which played correctly should attain 56.425% MWC. Misplayed, it attained 47.216%, so White is charged with an error of 9.210% MWC. The response was 4-2, which played correctly should attain 61.716% MWC. Misplayed, it attained 50.275%, so Blue is charged with an error of 11.441%.
White won one game, and Blue won one game. And here is what the match analysis says, in part:
| Game | Luck based FIBS rating diff. | Error based abs. FIBS rating |
| won by White | White -47.22 | White 1748.9, Blue 479.1 |
| won by Blue | White +288.55 | White 1839.3, Blue 1788.2 |
I don't see what these numbers are useful for. But neither do I see why Blue's error should count less because it was made after White's error, or why that should be an any more accurate method of calculating White's relative advantage over Blue.
If I'm correct about your real concern, then I think that part of the problem is a confusion between this concern and some of your comments about MWC which suggested that you, not everyone else, were misunderstanding MWC. For example, you wrote:
If you make 6 errors of 10% MWC ... [a]ll players wrongly believe that you lose 60% MWC. That means that you win -10% MWC.
Elsewhere, you indicated that one 60% MWC error should reduce your winning chances by 30%:
50% - (0.5 * (100-60)/100%) = 30%
but six separate errors costing 10% MWC each should reduce your winning chances by 23.4%:
50% - (0.5 * (100-10)/100%)^6) = 23.4%
Well, no. First of all, those unnamed players do indeed think that 1 * 60% = 6 * 10%. It's all the same to a bot. Either way, 60% MWC is lost. But we certainly do not think that giving away 60% MWC means we win a negative number of matches. That's impossible. We're not that dumb. What we do think is that if you give away 60% MWC by mistake, your winning chances are 60% lower than what they would have been if you hadn't made those mistakes.
Just to be clear, let's be sure we agree that it certainly is possible to give up 60% MWC (or more) in just one mistake. Here is such a position, in which the mistake reduces MWC by 64%:
The score (after 0 games) is: White 5, Blue 4 (match to 7 points). Blue to play 5-2
| White | 4 |
|---|---|
| |
| Blue | 7 |
Position ID: CQAAEAEAAAAAAA Match ID: QYnqAFAAIAAA | |
The right play here is 5/off 2/off, which makes the score 1-away 2-away, which gives Blue 67.7%% MWC. The wrong play is 5/3 3/off, which makes Blue's MWC 5.55% * 0.677 = 3.7%. Blue's error -- the bot will tell us -- has cost Blue 67.7 - 3.7 = 64% MWC. And how much lower is Blue's "winning chance" after making this mistake? Unsurprisingly, also 64% lower.
In short, a mistake can be made that costs more than 50% MWC, provided that best play attains greater than 50% MWC. And again, it's not at all clear to me why counting Blue's error as something other than 64% should be somehow more accurate or useful.
I want to say something about skill and luck. When you win a match, your MWC has gone from 50% to 100%, an increase of 50%. How is that possible? You got lucky, you played better, or both. If no errors are made, the increase is entirely due to luck. If your opponent gives away 10% MWC in error, the other 40% is due to your better luck. If you give away 10% and your opponent gives away 20%, then 10% is due to your net skill and the other 40% is due to your better luck.
In the 5-point match you mention, where the bot says you gave away 20% MWC and your opponent gave away 88%, you gained 68% MWC due to your superior skill. How is that possible, when gaining 50% MWC wins the match? Because you need to gain an additional 18% MWC to win because your opponent was luckier than you were.
You might explain why it "seems realistic" to you that you should win 73% of the time against this particular player. Then again, you might mention what other method you're comparing yours to, and what its prediction is.
Anyway, what's not due to error must be due to luck. What's not due to luck must be due to error. But bots evaluate error and luck separately, and neither evaluation is perfect. If they were perfect, MWC gained by net advantage in error and luck would always add up to 50% MWC. We know they don't. But your formula doesn't seem, really, to address that problem.
Finally, I want to turn again to the problem of the balls or marbles in the urn. I think that if I'm right about your real concern, then you completely obscure that concern by insisting that losing -10% MWC does not mean winning 10% less often -- as everyone else understands it. But in any case, you wrote:
I will try now to prove that it becomes 45%. In an urn there are 100 marbles, 50 of them are white and 50 are black. If you extract 10% * 100 = 10 marbles and paint them black and then put back in the urn how many white marbles will be in the urn now? Between 40 and 50 depending on how many white marbles you extract, but the mean is 45. If you try with 60% the mean is 20.
You already gave the same example except with 1 billion balls, and got a response, which as of now you've ignored. But I will state that I find both "proofs" unpersuasive.
I would first ask: why are the 100 marbles in the urn half white and half black? Well, only because they represent the half of matches you win and the half of matches you lose when each side makes no errors. I think that you should imagine that before the 100 marbles were half black and half white in the urn, they were not in the urn and they were colorless. As each marble was placed in the urn, the probability of it becoming either white or black was 50%. When 100 marbles had been placed in the urn, half were white and half were black. That represents what we can expect (in the long run) when nothing but luck affects the outcome of our matches -- when two perfect opponents each have 50% MWC. The only reason the marbles turn out to be half white and half black is that it has been determined in advance that each marble has a 50% chance of being either white or black.
What's the case when your MWC is only 40%, not 50%? Well, then as you place each marble in the urn, each marble has only a 40% chance of becoming white and a 60% chance of becoming black, and you end up, on average, with 40 white marbles and 60 black marbles.
That's why I said before, when you were talking about matches "known" to be won and lost, that I would like to use your time machine to see which matches are already lost and won, so I'd know when to make a meaningless error. I think your examples with urns have the same problem. We can fill another urn, if we like, with a 60/40 distribution of different marbles, but the marbles in the first urn are already divided 50/50. Their color is set -- we do know their colors -- and we can't change them.
Suppose you say: "here's an urn with 100 marbles in it. How many are white and how many are black?"
I'd have to say: "How could I possibly know? But tell me, what is the probability of any one marble placed in the urn being white?"
And then you could tell me that the probability was 0.5, in which case there ought to be, on average, 50 black and 50 white marbles. Or you could tell me that the probability was 0.4, in which case there ought to be, on average, 60 black marbles and 40 white marbles. But the probability of a marble being white can't be both 0.5 and 0.4. And it can't be the case that the probability was 0.5 and now is 0.4.
Now seriously you guys should change something in your schools if you don't understand that the winning percentage becomes 45% when you make an 10% MWC error.
Well, "seriously," that's not how everyone else seems to understand and use these terms, and although one possibility is that everyone but you is undereducated and you're the only smart guy here, that doesn't seem to be the most likely possibility. Frankly, I don't know how much more seriously you really expect to be taken by those you dismiss as ridiculing hypocrites. As always, I'll be happy to be shown to be wrong myself in any way, since being wrong is almost as good as being right, since otherwise we'd never have the pleasure of correcting any errors.