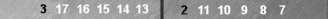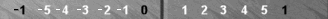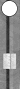This is a bonus Naccel 2 clarification (between post #8 and post #9) that is in response to a recent post from Lucky Jim.
I would be grateful for confirmation and views on the following few points -
Mirrors, Zigs and Zags
My understanding is that the Mirror applies in Naccel when you have two sets of checkers on opposite sides of the board. For the “standard” Mirror the set on the side with the home board for that colour’s checkers is always one pip closer to the bearoff tray.
Correct. For example, see the third and fourth diagrams here. With the mirror in the fourth diagram, you can march both points as many pips equally leftward as you like and the count remains 4 (the number of checkers in the mirror).
If you move a set of 2 checkers backwards 3 pips (zag) the count goes up by 1 (two checkers x 3 pips = 6 pips).
If you move a set of 2 checkers forward 3 pips (zig) the count goes down by 1 (two checkers x 3 pips = 6 pips).
Right, and right again. A mirror (of two points) counts 4. A zag (ninth diagram) counts 5, and a zig (third diagram) counts 3.
Am I correct that provided you keep them on opposite sides of the board you can move the set on either side of the board the three pips forward or backwards for the purposes of doing a count?
Yes, though I'd like to clarify that your goal is to instantly see (by the angle) these other-mirror formations as zig = 3 and zag = 5, rather than every time thinking "it would be a mirror of 4 if it were here, but since it is slid forward 3 pips it is a zig mirror of 3" (or "...since it is slid back 3 pips here it is a zag mirror of 5"). I realize this instant vision doesn't come all at once.
Points of a formation need to be on opposite sides of the board to be called a mirror, a zig or a zag. However, to be clear, there is no restriction on where you zig or zag (I'm using these z-terms in their verb forms now) two checkers, any more than there is a restriction on where you hop a single checker. Indeed, zigging or zagging are really just another form of hopping: two checkers 3 pips each (instead of one checker 6 pips).
In other words, you can freely cross sides of the board when hopping, zigging or zagging. For example...
| |
|---|---|
| Mirror | 4 |
| |
|---|---|
| Block | 3 |
The zig mirror and the block are based on the same underlying design: two checkers each on the fourth and fifth points of a quadrant field -- those points just happen to be in the same field now.
By the same token, starting from the mirror in the previous diagram (count of 4), you can zag the back point backwards, achieving a zag (count of 5), or you can zag the front point backwards (also getting a count of 5), which looks like this:
| |
|---|---|
| Midblock | 5 |
You can just as easily morph the blocks (of the last two diagrams) into zig mirrors and zag mirrors by employing the same technique in reverse. Just remember that when you zig (forward) you subtract 1 from the count, and when you zag (backward) you add 1 to the count.
Each time you make a movement (zig, zag, hop, shift, whatever), I recommend that you use it as an opportunity to learn or reinforce the counts of both the pre-move formation and the post-move formation; this will bring you closer to recalling them as instant counts the next time you see them.
| |
|---|---|
| 6(2) | |
Very good! For succinctness, you might consider using the term "near side" in your explanation, for example:
"n-3 and n15 is a Mirror of 4. The rest of the near side is a five-prime poof, and the blot counts 2(2). Total of 6(2)."
IMO, a slightly faster way is to mirror all three back checkers against the front, for a count of 6, and add the 2 pips necessary to create a poof. Total of 6(2).
For clarity, I've removed the mirrored checkers below (that gave the count of 6). Playing +2 pips (either n2 to n0, or n0 to n-2) restores the poof.
| |
|---|---|
| Poof this by moving +2 pips | (2) |
In term of white’s checkers I wasn’t sure of the best way to count this and would be interested in how others would tackle this.
| 1(2) | |
|---|---|
| |
Petter then added this +1 pip movement (i.e., getting roofer to S3) to n-3 to n0 (-3 pips) and four checkers on n1 to n0 (+ 4 pips) for a net of +2 pips. He added that to the triplet remaining on n2, which counts 1, for a total of 1(2).
Petter's alternative count also involved +1 pip for the roofer (poofing against the n-3 stack), then moved the n-3 spare 5 pips back to n2 (net of -4 pips) and counted 2 for the double-block. That's a total of 2(-4), which agrees with his 1(2) count above.
I try to make my shifts two-sided (shift and countershift) whenever possible, and it's amazing how often there is a dual purpose shift available. I chose this one:
| Poof-poof, Block, +2 pips | 1(2) |
|---|---|
| |
(Please excuse this not being posted with a Naccel numbered board but I have yet to master).
Matt has created an excellent FAQ that explains how to create a Naccel-numbered board. Perhaps this isolated explanation will also help elucidate:
After you've copied the Gnu diagram html, look for the word "Board," which is sitting on its own line above the compacted part of the html. About three lines below that, find the word "high" or "low" and in its place type "naccel2_far" -- that will change the upper point number line to Naccel.
Then look for the phrase "End Board," sitting by itself below the compacted part of the html. About four lines above that, find the word "low" or "high" and in its place type "naccel2_near" -- that will change the lower point number line to Naccel.
The instructions above give you a Naccel board numbered from Blue's perspective. If instead you want it numbered from White's perspective, invert "far" and "near."
Please try posting a Naccel diagram so that I can see you've succeeded.
Final query in this post – in practical terms could Nack confirm how far up the 6 times table a Naccel counter should know for the calculations likely to be performed over the board?
You already know this part but I'll review for others: To convert a Naccel count to a traditional count, multiply by 6, add (or subtract) the leftover pips and add 90. For example Blue's count of 6(2) here converts to 6*6 + 2 + 90 = 128, and White's count of 1(2) converts to 1*6 + 2 + 90 = 98.
When you practice converting Naccel to traditional, start by memorizing just: -5 = 60, 0 = 90, 5 = 120, and 10 = 150. That way when your count is "1" you'll see it's 90 + 6 = 96, when your count is "9" you'll see its 150 - 6 = 144, etc., and before long you'll know all the 6-counts (so that the conversion process will be nothing more than adding or subtracting the baby pips).
That said, aside from counting practice (to confirm your Naccel counts with trad/decimal totals, which are currently the only way that books and bots display pipcounts), the only reason to convert to trad is that you're in a straight race and the difference between totals is around 10 pips (so that you might need to apply a race formula). In that case, note that you need convert only one side to a trad total (you already know the difference in pips).
Later, I'll coach you on the Naccel race formula, which I am in the process of recalibrating, and then you won't be converting to trad at all (unless you want to).
Many thanks
Jim
Any time
Nack