                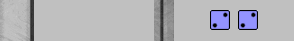                  |
| ||||
| XGID=---BBBC---A-dC----Babbbbb-:1:-1:1:22:0:0:3:0:10 | |||||
43S-44P-21@-55J-55C-52I-62P-33P-31P-11E-C-21D-55R-22 | |||||
| 1. | Rollout1 | 13/11 6/2 4/2 | eq: -0.5309 | |||
| ||||||
| 2. | Rollout1 | 13/11 10/8 6/2 | eq: -0.5331 (-0.0023) | |||
| ||||||
| 3. | Rollout2 | 10/2 | eq: -0.5344 (-0.0035) | |||
| ||||||
| 4. | Rollout2 | 13/7 4/2 | eq: -0.5349 (-0.0040) | |||
| ||||||
| 5. | Rollout3 | 6/2(2) | eq: -0.5352 (-0.0043) | |||
| ||||||
| 6. | Rollout3 | 13/7 10/8 | eq: -0.5363 (-0.0055) | |||
| ||||||
| 7. | Rollout3 | 13/9 6/2 | eq: -0.5370 (-0.0062) | |||
| ||||||
| 8. | Rollout4 | 10/8 6/2 4/2 | eq: -0.5385 (-0.0076) | |||
| ||||||
| 9. | Rollout3 | 13/9 10/8 4/2 | eq: -0.5396 (-0.0088) | |||
| ||||||
| 10. | Rollout3 | 13/9 4/2(2) | eq: -0.5410 (-0.0102) | |||
| ||||||
| 11. | Rollout5 | 13/7 6/4 | eq: -0.5452 (-0.0143) | |||
| ||||||
| 12. | Rollout4 | 13/9 10/8 6/4 | eq: -0.5493 (-0.0185) | |||
| ||||||
| 13. | Rollout4 | 13/5 | eq: -0.5499 (-0.0191) | |||
| ||||||
| 14. | Rollout4 | 13/11 10/4 | eq: -0.5500 (-0.0192) | |||
| ||||||
| 15. | Rollout4 | 13/9 10/6 | eq: -0.5515 (-0.0206) | |||
| ||||||
| 1 41472 Games rolled with Variance Reduction. Dice Seed: 1019915 Moves: 3-ply, cube decisions: XG Roller 2 31104 Games rolled with Variance Reduction. Dice Seed: 1019915 Moves: 3-ply, cube decisions: XG Roller 3 20736 Games rolled with Variance Reduction. Dice Seed: 1019915 Moves: 3-ply, cube decisions: XG Roller 4 5184 Games rolled with Variance Reduction. Dice Seed: 1019915 Moves: 3-ply, cube decisions: XG Roller 5 10368 Games rolled with Variance Reduction. Dice Seed: 1019915 Moves: 3-ply, cube decisions: XG Roller | ||||||
With double 2s in the position above, it never occurred to me that n.(near, 13/11 6/2 4/2) might be the best play. I merely used it as a way of reaching the position diagrammed in the Ho-Hum 61 post in 14 rolls (without it and the 51 play that followed it, I needed 15 rolls), while making sure that all moves are "well played" (within .02 of best).
OTB, I would have played the natural-looking n (near, 13/11 10/8 6/2). Okay, that apparent error is a mere .002+ in equity, but my concern is that XG's rollout projects that breaking the 4pt to cover the 2pt is better—with 99.9% confidence—and I don't understand why.
Below is additional support for NOT shifting with 4/2. It is a rollout of the 51 play made immediately following it (just prior to the Ho-Hum 61 position), and a second rollout of the 51 choice that White would have been faced with if Blue had played his 22 more naturally (with 10/8).
                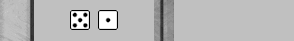                  |
| ||||
| XGID=--BBABB---AAdB----Babbbbb-:1:-1:-1:51:0:0:3:0:10 | |||||
43S-44P-21@-55J-55C-52I-62P- | |||||
| 1. | Rollout1 | 13/8 6/5 | eq: +0.384 | |||
| ||||||
| 2. | Rollout1 | 6/1 5/4 | eq: +0.370 (-0.015) | |||
| ||||||
| 1 10368 Games rolled with Variance Reduction. Dice Seed: 44860624 Moves: 3-ply, cube decisions: XG Roller | ||||||
                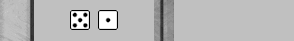                  |
| ||||
| XGID=--ABBBB-A--AdB----Babbbbb-:0:0:-1:51:0:0:3:0:10 | |||||
43S-44P-21@-55J-55C-52I-62P- | |||||
| 1. | Rollout1 | 6/1 5/4 | eq: +0.284 | |||
| ||||||
| 2. | Rollout1 | 13/8 6/5 | eq: +0.243 (-0.041) | |||
| ||||||
| 1 5184 Games rolled with Variance Reduction. Dice Seed: 44860624 Moves: 3-ply, cube decisions: XG Roller | ||||||
In the first (left-hand) position, White is emboldened to start the 8pt, mainly so that her future rolls rate to play more safely. For example, she might cover the 8pt and subsequently clear the midpoint with 54 53 52 while leaving a single shot, or avoid a later double-blot disaster (e.g., with 51, 42 or 41), or just having a checker or two advanced to the 8pt will help her manage some of her rolls (such as the next 51 or two consecutive small 4s, etc.) She also keeps her 5pt.
White's ace-shot is worth the risk only if Blue has downgraded her board as in the left-hand position. White's gain in equity is .015, and thus .015/18 = .0008 has to be charged to Blue's 4/2 play (because 51 is rolled 1/18 of the time). In other words, the 4/2 play is .0023 ahead of the 10/8 play in spite of the .0008 penalty it incurs from White's correctly bold response of 51. This means that we are actually looking for .0023 + .0008 = .0031 of equity to explain.
An upside to 4/2 (versus 10/8) is in the greater likelihood of making the fifth point in the board a roll sooner, due to the ability to cover with 6s, 52 43 (and sometimes 54) instead of just 6s and 54. Let's call the difference 3 numbers, which occur 1/12 of the time. However, the only two-roll combinations I see with which White will leave a shot are 51+65 and 51+11, and these have already been accounted for by (the difference in) the 51 rollouts. [Even if not, the effect would only be (6/1296*25/36)/12 = .0003, and for that only the subset of games swung by not having covered the 2pt!]
We are still left with .0031 of equity to explain. Anyone have an idea?
Finally, consider the fourth-ranked play of 13/7 4/2, which leaves both the 4pt and 2pt slotted. In this case, White gains .068 in equity by leaving a shot with 51 (according to the XGR++ evaluation below). Hmm... so, despite sacrificing .068 / 18 = .0038 in the immediate 51 (plus whatever it might cost to have 11 fewer numbers that make a five-point board on the following roll), Blue's 13/7 6/4 play is only .0017 worse than the solid 13/11 10/8 6/2? This means that the double-blotting move gains .0021 in other variations... somehow.
Is it possible that bots have a built-in bias towards slightly unsound shifts and multiple slots (that modern players try to mimic) in preparation for a shot that somehow don't correspond to real equity? (For example, it might sometimes make less bold plays than it should for the opponent that don't take full advantage of the player's temporarily compromised board.)
Food for thought.
Nack
                                  |
| ||||
| XGID=--ABABCA--A-dB----Babbbbb-:1:-1:-1:51:0:0:3:0:10 | |||||
White's bold 51 gains substantial equity | |||||
| 1. | XG Roller++ | 13/8 6/5 | eq: +0.462 | |||
| ||||||
| 2. | XG Roller++ | 6/1 5/4 | eq: +0.395 (-0.068) | |||
| ||||||
eXtreme Gammon Version: 2.10