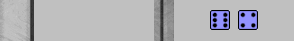           
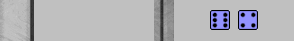 
 | | White is Player 2
score: 0
pip: 92 | | Unlimited Game | pip: 120
score: 0
Blue is Player 1 |
|
| XGID=-aBBBBBA--A------c-cbCdb--:1:-1:1:64:0:0:0:0:10 |
| Blue to play 64 |
| 1. | Rollout1 | 21/11 | eq: +0.2715 |
| Player:
Opponent: | 68.72% (G:9.11% B:0.26%)
31.28% (G:11.54% B:0.26%) | Conf.: ±0.0024 (+0.2690...+0.2739) - [100.0%]
Duration: 8 minutes 38 seconds |
|
| 2. | Rollout1 | 10/6 7/1* | eq: +0.1807 (-0.0908) |
| Player:
Opponent: | 64.76% (G:8.86% B:0.16%)
35.24% (G:9.29% B:0.15%) | Conf.: ±0.0030 (+0.1776...+0.1837) - [0.0%]
Duration: 7 minutes 02 seconds |
|
| 3. | Rollout1 | 21/15 7/3 | eq: +0.1365 (-0.1350) |
| Player:
Opponent: | 63.08% (G:7.14% B:0.19%)
36.92% (G:6.82% B:0.12%) | Conf.: ±0.0030 (+0.1335...+0.1395) - [0.0%]
Duration: 7 minutes 11 seconds |
|
| 4. | Rollout1 | 21/15 10/6 | eq: +0.1139 (-0.1576) |
| Player:
Opponent: | 62.87% (G:8.05% B:0.21%)
37.13% (G:11.18% B:0.20%) | Conf.: ±0.0027 (+0.1112...+0.1166) - [0.0%]
Duration: 7 minutes 01 second |
|
| |
1 5184 Games rolled with Variance Reduction.
Dice Seed: 7671034
Moves: 3-ply, cube decisions: XG Roller
|
Rollout by Taper_Mike
2015-Dec-25
eXtreme Gammon Version: 2.10.199.2658
53P-33B-63S-51K-31-43P-66Z-53S-61O-21E-51p-52C-51J-43D-64O-C-44J-51Z-43P-F-43P-41E-64-n-tm.xgp
n[S J91 c135 C158] "<=5
n[S J92 c127 C157] "&e |
eXtreme Gammon Version: 2.10
In most positions of this ilk, attacking is automatic. By hitting, you force the opponent to get lucky twice. First, he must roll an ace to enter. Second, he must roll a 6 to escape. If you leave him unmolested, he only needs to get lucky once, by rolling a 6.
So why is it a whopper to hit in this position? One explanation is the danger of cracking. Blue will face four cracking numbers (44, 22, and 42) after he hits. Four does not sound like a large number, but it represents 11% of all possibilities. Here is a variant where there are none.

 | | White is Player 2
score: 0
pip: 92 | | Unlimited Game | pip: 117
score: 0
Blue is Player 1 |
|
| XGID=-aBBBBBA--A------cAcbBdb--:1:-1:1:64:0:0:0:0:10 |
| Blue to play 64 |
| 1. | Rollout1 | 10/6 7/1* | eq: +0.3576 |
| Player:
Opponent: | 71.58% (G:10.18% B:0.16%)
28.42% (G:8.97% B:0.16%) | Conf.: ±0.0031 (+0.3545...+0.3607) - [100.0%]
Duration: 6 minutes 06 seconds |
|
| 2. | Rollout1 | 18/14 7/1* | eq: +0.3395 (-0.0181) |
| Player:
Opponent: | 71.18% (G:10.05% B:0.18%)
28.82% (G:10.56% B:0.30%) | Conf.: ±0.0031 (+0.3364...+0.3426) - [0.0%]
Duration: 6 minutes 38 seconds |
|
| 3. | Rollout1 | 18/8 | eq: +0.2276 (-0.1300) |
| Player:
Opponent: | 66.93% (G:8.59% B:0.23%)
33.07% (G:10.16% B:0.23%) | Conf.: ±0.0022 (+0.2253...+0.2298) - [0.0%]
Duration: 7 minutes 18 seconds |
|
| |
1 5184 Games rolled with Variance Reduction.
Dice Seed: 12074957
Moves: 3-ply, cube decisions: XG Roller
|
eXtreme Gammon Version: 2.10
Here is a variant where Blue will face two cracking numbers (22 and 33) if he plays 10/6 7/1*.

 | | White is Player 2
score: 0
pip: 89 | | Unlimited Game | pip: 120
score: 0
Blue is Player 1 |
|
| XGID=-aBBBBBA--A-------ccbCdb--:1:-1:1:64:0:0:0:0:10 |
| Blue to play 64 |
| 1. | Rollout1 | 21/17 7/1* | eq: +0.3433 |
| Player:
Opponent: | 72.04% (G:8.34% B:0.19%)
27.96% (G:11.41% B:0.25%) | Conf.: ±0.0032 (+0.3401...+0.3465) - [100.0%]
Duration: 7 minutes 24 seconds |
|
| 2. | Rollout1 | 21/11 | eq: +0.2934 (-0.0499) |
| Player:
Opponent: | 69.51% (G:9.40% B:0.29%)
30.49% (G:13.76% B:0.29%) | Conf.: ±0.0024 (+0.2909...+0.2958) - [0.0%]
Duration: 8 minutes 56 seconds |
|
| 3. | Rollout1 | 10/6 7/1* | eq: +0.2288 (-0.1145) |
| Player:
Opponent: | 67.02% (G:7.52% B:0.16%)
32.98% (G:9.66% B:0.13%) | Conf.: ±0.0034 (+0.2254...+0.2322) - [0.0%]
Duration: 6 minutes 37 seconds |
|
| |
1 5184 Games rolled with Variance Reduction.
Dice Seed: 12074957
Moves: 3-ply, cube decisions: XG Roller
|
eXtreme Gammon Version: 2.10
The other factor cited in this thread is that Blue will build a prime more quickly by not hitting. Is that more important than the cracking numbers? Both have an effect, but my sense is that the cracking numbers are the primary factor.
Mike